Формулы сокращенного умножения:степень суммы и степень разности

Схема «слева направо»

Пусть количество цифр в числе   n  есть   l(n) = t :   \left( n_{t-1} \dots n_{0} \right)_{2} .  Для каждого   k \in \left  обозначим   m_{k} = \left( n_{t-1} \dots n_{k} \right)_{2} .

Если   k = 0 , то   m_k = n  и поэтому   a ^{m_k} = a^{n} .

Если   0 < k \leq t-1 , то

m_{k-1} = \left( n_{t-1} \dots n_{k} n_{k-1} \right)_{2} = 2\left( n_{t-1} \dots n_{k} \right)_{2} + n_{k-1}= 2 m_{k} + n_{k-1}

и поэтому

a^{m_{k-1}} = \left( a^{m_{k}} \right) ^ {2} a^{n_{k-1}} = \begin{cases}\left(a^{m_{k}}\right)^{2} & \text{} n_{k-1} = 0 \\a * \left(a^{m_{k}}\right)^{2} & \text{} n_{k-1} = 1 \end{cases}

Получаем следующий алгоритм:

Python

def pow(a,n):
# Обработка тривиального случая
if (n == 0):
return e()
# Стадия препроцессинга
D = []
while (n > 0):
D.append(n % 2)
n = n // 2
t = len(D)
# Стадия вычислений
r = a
for k in range(t-2,-1,-1):
r *= r
if (D == 1):
r *= a
return r

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

defpow(a,n) # Обработка тривиального случая if(n==) returne() # Стадия препроцессинга D= while(n>) D.append(n%2) n=n2 t=len(D) # Стадия вычислений r=a forkinrange(t-2,-1,-1) r*=r if(Dk==1) r*=a returnr

Отмечу, что процесс «накопления» показателя степени в данном алгоритме по сути идентичен процессу вычисления значения многочлена  \sum_{k=0}^{t}n_{k}x^{k}  в точке   x = 2  по схеме Горнера.

Главным преимуществом данного алгоритм перед алгоритмом по схеме «справа налево» является тот факт, что на стадии домножения (если текущая цифра —  единица), умножение всегда происходит на один и тот же элемент. Иногда это позволяет существенно сэкономить время, затрачиваемое на умножение. Например, в тестах простоты встречается ситуация степени с малым основанием и большим показателем. В этом случае умножение на основание является операцией существенно более быстрой, чем умножение на произвольное число, которое может возникнуть в схеме «справа налево».Оценка времени. Деление на   2  можно считать быстрой операцией. Поэтому, игнорируя детали работы со списками, время на препроцессинг можно оценить как линейно зависящее от   l(n) . Оценим количество возведений в квадрат / умножений. В случаях   n = 0  и   n = 1   не производится ни возведений в квадрат, ни умножений.  Если же   n > 1 , то цикл  for  в стадии вычислений отработает   l(n)-1  шаг и на каждом из них будет произведено возведение в квадрат. При этом «на каждой единице», кроме старшей, будет произведено умножение на   a . В итоге получаем, что при   n > 1  алгоритму требуется   l(n) — 1  возведений в квадрат и   s(n) — 1  обычных умножений, где   l(n)  —  количество цифр в двоичной записи числа   n , s(n)  —  количество единиц в двоичной записи   n .

Как возвести в отрицательную степень дробь

Запомните!

Чтобы возвести дробь в отрицательную степень нужно:

• «перевернуть» дробь;
• заменить отрицательную степень на
  положительную;
• возвести дробь в положительную степень.

Пример. Требуется возвести в отрицательную степень дробь.

Возведем дробь в положительную степень по правилу возведения дроби в положительную степень.
Т.е. возведем и числитель «», и знаменатель «» в третью степень.

Для более грамотного ответа запишем полученный результат в виде десятичной дроби.

Как возвести отрицательное число в отрицательную степень

Как и при возведении отрицательного числа в положительную степень, в первую
очередь необходимо определить конечный знак результата возведения в степень. Вспомним основные правила еще раз.

Запомните!

Отрицательное число, возведённое в
чётную степень, — число
положительное.

Отрицательное число, возведённое в
нечётную степень, — число
отрицательное.

Пример.

Перевернем число «» и заменим отрицательную степень
«» на положительную
«».

Так как степень «» — четная, значит, результат возведения в степень будет
положительный. Поэтому
убираем знак минуса при раскрытии скобок.

Далее откроем скобки
и возведем во вторую степень и числитель «», и знаменатель «».

Как возвести отрицательную дробь в отрицательную степень

Конечный знак результата возведения в степень отрицательной дроби определяется по тем же правилам, что и для целого отрицательного числа.

Запомните!

Отрицательная дробь, возведённая в
чётную степень, — дробь
положительная.

Отрицательная дробь, возведённая в
нечётную степень, — дробь
отрицательная.

По правилу возведения дроби в отрицательную степень перевернем дробь и заменим отрицательную степень «» на положительную
«».

Теперь определим конечный знак результата возведения в «» степень.

Степень «» — нечетная, значит, по правилу возведения отрицательного числа в степень дробь
останется отрицательной.

Нам остается только раскрыть скобки и возвести в степень и числитель «», и знаменатель
«» в третью степень.

Для окончательного ответа выделим целую часть из дроби.

Рассмотрим другой пример возведения отрицательной дроби в отрицательную степень.

Правило возведения отрицательного числа в степень гласит: если степень четная, значит, результат возведения
будет положительным.

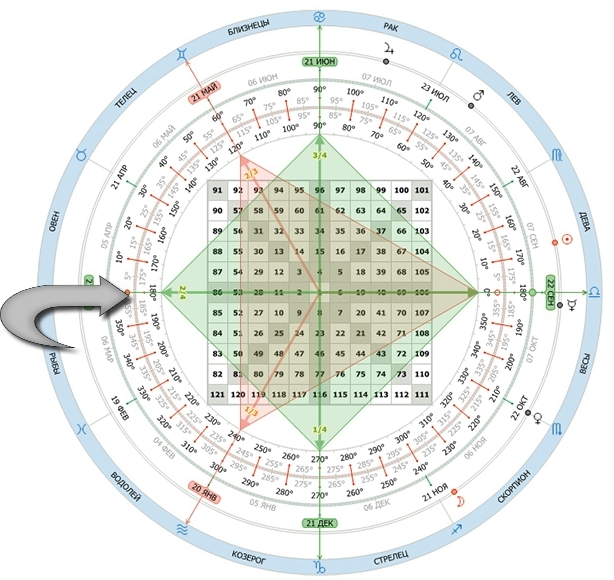
Прогресс движения чисел в Квадрате Ганна

Следуя Квадрату девяти, прогресс движения к квадрату нечётного числа к квадрату чётного числа или наоборот даёт нам сначала числа равные 1/4 квадрата, а затем срединные числа – 1/2 квадрата, потом числа равные 3/4 квадрата. Числа равные 1/4 расположены на правой и на левой горизонтальных осях квадрата.

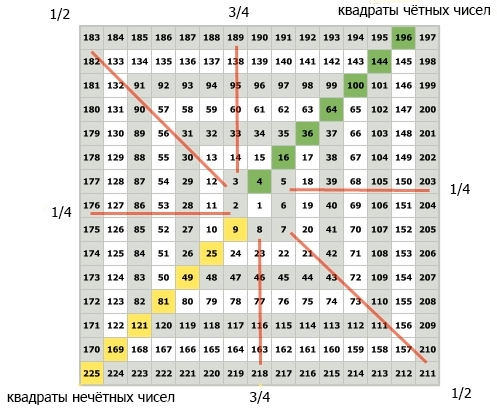прогресс движения чисел в квадрате

Например, между чётным квадратом 196 и нечетным 225 первое четвертичное число равно 203,25. Числа равные 3/4 квадрата расположены на верхней и нижней вертикальных осях.

Например, 3/4 между нечетным квадратом 169 и чётным 196 равно 189 и 25.

Числа равные 1/4 и 3/4 квадрата не являются целыми числами. Числа подобные 203,25 не отображаются на квадрате. Они находятся между целыми числами, составляющими Квадрат девяти. На этом же примере представлен такой же квадрат, но теперь эти точки используются, чтобы разделить полный оборот на 8 частей.

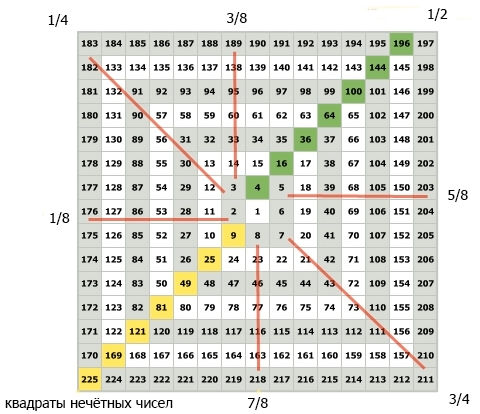1/8 Квадрата Ганна

В данном случае мы получаем числа равные 1/8 квадрата.

Ввод команд в наш онлайн-калькулятор с клавиатуры ПК

Работа с калькулятором довольно проста и не вызовет сложностей ни у кого. Для ввода цифр используются клавиши компьютерной клавиатуры с цифрами или цифровые клавиши справа на дополнительной панели.

Чтобы стереть неправильно введенный символ используйте клавишу .

Чтобы получить результат сложения или вычитания, жмите клавишу равно – используйте для этого .

Чтобы использовать знак «плюс», жмите на клавиатуре клавишу . Она расположена на дополнительной клавиатуре справа вверху.

Чтобы использовать знак «минус», жмите на клавиатуре клавишу . Она расположена сверху или на дополнительной клавиатуре.
Для умножения или деления используйте знаки и [ / ] соответственно, которые расположены на боковой клавиатуре.

Чтобы обнулить все расчеты или начать подсчет сначала, нажмите , на верхней клавиатуре или же используйте кнопку на боковой клавиатуре.

Простые примеры вычислений, используя калькулятор онлайн с корнями
Возвести число 2 в степень 3: 23. Результат — 8.
Вычисление квадратного корня числа 625: 625 . Результат — 25.
Вычисление процента от числа: 1000 20 . Результат — 200.
Прибавление процента к числу: 800 25 . Результат — 1000.
Вычитание процента из числа: 800 25 . Результат — 600.

Часто задаваемые вопросы

У пользователей достаточно часто возникает вопрос: почему если на калькуляторе посчитать 3+3х3=18, то калькулятор, вероятно, считает неверно? Нет, калькулятор считает абсолютно правильно. При вводе очередного математического действия онлайн калькулятор делает подитог

Рекомендуем при проведении подсчетов обращать внимание на дисплей текущих действий. Он расположен справа под основным дисплеем

А теперь попробуем посчитать:

3+3=6, подитог 6. Далее: 6х3=18. Правильный ответ – 18. Ошибок в данном случае нет.

Из истории возникновения калькуляторов

Основным прародителем современного калькулятора считается абак – доска со специальными углублениями, по которым перемещали счетные метки (в большинстве случаев это были косточки или камни). Впервые абак был замечен в Древнем Вавилоне около 3000 лет до н.э. В Древней Греции такой вычислительный прибор появился только в V веке до н.э.

В России абак появился только в 16 веке. Первые русские счеты были выполнены из натуральной древесины. Счетными метками были вишнёвые косточки.

Если вам понравились наши сервисы, поделитесь ими с друзьями! Нет ничего проще, когда за вас делает расчет онлайн калькулятор!
Помимо обычного калькулятора у нас на сайте вы можете встретить: калькулятор корней (в том числе вы можете выполнить умножение корней, деление, сложение и вычитание квадратных корней), калькулятор онлайн с корнями и дробями (математический) и прочие!

Шаблонный калькулятор цены и времени

Квадрат 9 Ганна – шаблонный калькулятор цены и времени

В 1920 году Ганном был создан квадрат девяти (Квадрат Ганна). Это своего рода финансовый калькулятор для исследований и торговли. Квдрат девяти Ганн называл шаблонным калькулятором цены и времени. Квдрат девяти бессомненно является одним из самых популярных и таинственных инструментов рынка. Есть в нём нечто такое, что заинтриговывает абсолютно всех, кто с ним хоть раз сталкивался. Будь то профессионал или начинающий трейдер.

Про методы использования квадрата 9 Ганна написано много всевозможных статей и материалов. Но практически не в одной из этих работ не дано полного объяснения по работе с этим уникадьным инструментом. Каждый кто пытался изучать квадрат 9-ти наверняка задавался вопросом: Что это ? Просто обещание больших заработков для тех кто поймёт секретный код, заложенный в калькуляторе легендарного трейдера? Или это намного больше нежели просто калькулятор – нечто, что откроет путь великого познания окружающей нас действительности, включая финансовые рынки.

Во время знакомства с Квадратом 9-ти, начинаешь понимать, что его использование простирается далеко вне того, что бы быть просто интересным торговым инструментом легендарного предсказателя

Который можно использовать не только в качестве математического, но и что не мало важно, в качестве астрономического калькулятора предсказывающего будущее

Геометрическая прогрессия

Формулы n-го члена геометрической прогрессии:

Соотношение между тремя соседними членами геометрической прогрессии:

Формула суммы геометрической прогрессии:

Формула суммы бесконечно убывающей геометрической прогрессии:

Свойство геометрической прогрессии:

Практика суждения

Вы запрограммированы судить; у вас есть личные эмоции и чувства, которые судят. Даже если вы стремитесь быть непредвзятым, у вас все равно будут вещи, которые вы считаете «хорошими», а другие — «плохими».

Хорошая новость заключается в том, что вы можете сознательно приложить усилия, чтобы отложить суждение в сторону, и со временем они будут становиться все меньше и меньше. С теми, кого вы любите, это часто сложнее, чем проще. Почему вы судите о них больше, чем о незнакомцах? Потому что вы любите их больше. Вы видите хорошее внутри более ясным зрением.

Попробуйте напомнить себе о двух важных факторах:

1. Каждый человек делает все возможное на своем уровне сознания.

2. Мы все светлые и темные. Независимо от того, насколько удивителен человек, у него есть негативные моменты. Если смотреть под правильным углом, то эти негативные моменты могут привести к удивительной эволюции и личностному росту.

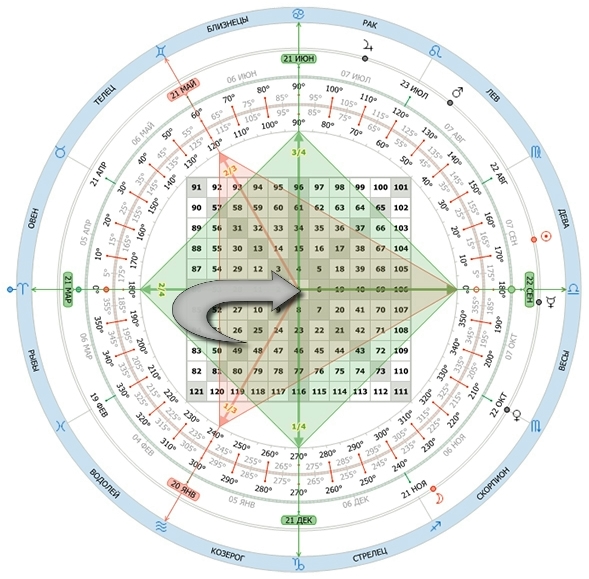
Из чего состоит Квадрат Ганна

Базовый Квадрат Ганна имеет два набора чисел. Первый набор расположен на окружности, находящейся снаружи квадрата.

Внешняя шкала у Квадрата Ганна

Второй набор находится на плоскости квадрата.

Внутренний набор чисел в Квадрате Ганна

Ганн разделил окружность на градусы. Кроме того он добавлял на окружность дни года и 24 часа дня.

Весеннее равноденствие – 21 марта, совпадает с отметкой 0 градусов, когда солнце находится в овне. Этот день называют первым днём весны и началом естественного года.

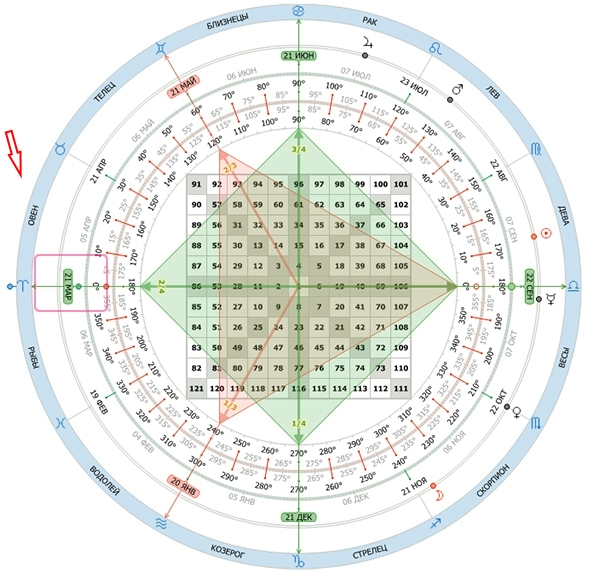Весеннее равноденствие 21 марта на шкале Квадрата 9

Летнее солнцестояние – 21 июня совпадает с отметкой 0 градусов, когда солнце находится в раке. Этот день называют самым долгим днём года для северного полушария.

Осеннее равноденствие – 22 сентября совпадает с отметкой 0 градусов, когда солнце находится в весах. С этой даты начинается сезон падений и солнце буквально начинает падать внизу экватора Земли.

И наконец зимнее солнцестояние – 21 декабря совпадает с отметкой 0 градусов, когда солнце находится в козероге. Это самый короткий день года в северном полушарии отмечающийся зоной зимы.

Данная разметка показывает нам, что даты не делят круг на равные части. От весеннего равноденствия до летнего солнцестояния промежуток составляет 92 дня. От летнего солнцестояния до осеннего равноденствия – 93 дня. От осеннего равноденствия до зимнего солнцестояния – 90 дней. И наконец от зимнего солнцестояния до осеннего равноденствия – также 90 дней. В сумме это составляет ровно 365 дней.

Комплекс операций инженерного калькулятора

Встроенный математический калькулятор поможет вам провести самые простые расчеты: умножение и суммирование, вычитание, а также деление. Калькулятор степеней онлайн быстро и точно возведет любое число в выбранную вами степень.

Представленный инженерный калькулятор содержит в себе все возможные вариации онлайн программ для расчетов. Kalkpro.ru содержит тригонометрический калькулятор (углы и радианы, грады), логарифмов (Log), факториалов (n!), расчета корней, синусов и арктангенсов, косинусов, тангенсов онлайн – множество тригонометрический функций и не только.

Работать с вычислительной программой можно онлайн с любого устройства, в каждом случае размер интерфейса будет подстраиваться под ваше устройство, либо вы можете откорректировать его размер на свой вкус.

Ввод цифр производится в двух вариантах:

• с мобильных устройств – ввод с дисплеем телефона или планшета, клавишами интерфейса программы
• с персонального компьютера – с помощью электронного дисплея интерфейса, либо через клавиатуру компьютера любыми цифрами

Решение уравнений методом подбора корня

Необязательно преобразовывать ур-ние, чтобы найти его корни. Одним из приемов решения целых уравнений является метод подбора корня. Ведь если надо доказать, что какое-то число – это корень ур-ния, достаточно просто подставить это число в ур-ние и получить справедливое равенство!

Пример. Докажите, что корнями ур-ния

х3 – 2х2 – х + 2 = 0

являются только числа (– 1), 1 и 2.

Решение. Подставим в ур-ние каждую из предполагаемых корней и получим справедливое равенство. При х = – 1 имеем:

(– 1)3 – 2(– 1)2 – (– 1) + 2 = 0

–1 – 2 + 1 + 2 = 0

0 = 0

При х = 1 получаем:

13 – 2•12 – 1 + 2 = 0

1 – 2 – 1 + 2 = 0

0 = 0

Наконец, рассмотрим случай, когда х = 2

23 – 2•22 – 2 + 2 = 0

8 – 8 – 2 + 2 = 0

0 = 0

Исходное ур-ние имеет 3-ю степень, поэтому у него не более 3 корней. То есть других корней, кроме (– 1), 1 и 2 , у него нет.

Конечно, просто так подобрать корни довольно тяжело. Однако есть некоторые правила, которые помогают в этом. Для начала введем понятие коэффициентов уравнения.

Понятно, что ур-ние Р(х) = 0 в общем виде можно записать так:

аxn + a₁xn–1 + … + а_n–1х + а_n = 0

Числа а, а₁, а₂,…а_nи называют коэффициентами уравнений.

Например, для уравнения

5х4 – 7х3 + 9х2 – х + 12 = 0

коэффициенты равны

а = 5

а₁ = – 7

а₂ = 9

а₃ = – 1

а₄ = + 12

Если одна из слагаемых «пропущено» в уравнении, то считают, что коэффициент перед ним равен нулю. Например, в ур-нии

х3 + 2х – 15 = 0

нет слагаемого с буквенной частью х2. Можно считать, что ур-ние равносильно записи

х3 + 0х2 + 2х – 15 = 0

где слагаемое х2 есть, но перед ним стоит ноль. Тогда коэффициент а₁ = 0.

Для обозначения первого коэффициента а может использоваться термин старший коэффициент, а для последнего коэффициента а_n – термин «свободный член» или «свободный коэффициент».

Изучение коэффициентов ур-ния помогает быстрее подобрать корень. Существует следующая теорема:

Докажем это утверждение. Пусть m – это целый корень уравнения с целыми коэффициентами

аxn + a₁xn–1 + … + а_n–1х + а_n = 0

Тогда можно подставить туда число m и получить верное равенство:

аmn + a₁mn–1 + … + а_n–1m + а_n = 0

Поделим обе его части на m и получим

аmn–1 + a₁mn–2 + … + а_n–1 + а_n/m = 0

Справа – целое число (ноль), значит, и сумма чисел слева также целая. Все числа аmn–1, a₁mn–2, а_n–1, очевидно, целые (так как и целыми являются и m, и все коэффициенты). Значит, и число а_n/m должно быть целым. Но это возможно лишь в том случае, если m является делителем числа а_n.

Из доказанной теоремы следует, что при подборе корней ур-ния достаточно рассматривать только те из них, которые являются делителями свободного члена. При этом следует учитывать и отрицательные делители.

Пример. Найдите целые корни уравнения

2х4 – х3 – 9х2 + 4х + 4 = 0

Решение. Все коэффициенты ур-ния – целые, а потому целый корень должен быть делителем свободного члена, то есть числа 4. Делителями четверки являются 1 и (– 1), 2 и (– 2), 4 и (– 4). Подставляя каждое из этих чисел в ур-ние, получим верные равенства только для чисел 1, 2 и (– 2):

2•14 – 13 – 9•12 + 4•1 + 4 = 2 – 1 – 9 + 4 + 4 = 0

2•24 – 23 – 9•22 + 4•2 + 4 = 32 – 8 – 36 + 8 + 4 = 0

2•(– 2)4 – (– 2)3 – 9•(– 2)2 + 4(– 2) + 4 = 32 + 8 – 36 – 8 + 4 = 0

Таким образом, только эти числа и могут быть целыми корнями ур-ния. Так как мы рассматриваем ур-ние 4 степени, то, возможно, у него помимо 3 целых корней есть ещё один дробный.

Ответ: 1; 2; (– 2).

Пример. Решите ур-ние

0,5х3 + 0,5х + 5 = 0

Решение. У ур-ния дробные коэффициенты. Умножим обе части равенства на 2 и получим ур-ние с целыми коэффициентами:

0,5х3 + 0,5х + 5 = 0

(0,5х3 + 0,5х + 5)•2 = 0•2

х3 + х + 10 = 0

Попытаемся подобрать целый корень ур-ния. Он должен быть делителем свободного члена, то есть десятки. Возможными кандидатами являются числа 1 и (– 1), 2 и (– 2), 5 и (– 5), 10 и (– 10). Подходит только корень х = – 2:

(– 2)3 + (– 2) + 10 = – 8 – 2 + 10 = 0

Обратим внимание, что в левой части ур-ния стоит сумма функций, возрастающих на всей числовой прямой: у = х3 и у = х + 10. Значит, и вся левая часть х3 + х + 10 монотонно возрастает

Это значит, что у ур-ния есть только один корень, и мы его нашли ранее подбором.

Ответ: – 2

Ещё быстрее можно узнать, является ли единица корнем уравнения.

Докажем это. Подставим в ур-ние

аxn + a₁xn–1 + … + а_n–1х + а_n = 0

значение х = 1. Так как единица в любой степени равна самой единице, то получим:

а1n + a₁1n–1 + … + а_n–11 + а_n = 0

а + a₁ + … + а_n–1 + а_n = 0

Получили равенство, в котором слева стоит сумма коэффициентов, в справа – ноль. Если сумма коэффициентов действительно равна нулю, то равенство верное, а, значит, единица является корнем ур-ния.

Пример. Укажите хотя бы 1 корень ур-ния

499х10 – 9990х7 + 501х6 – 10х5 + 10000х4 – 1000 = 0

Решение. Заметим, что при сложении коэффициентов ур-ния получается 0:

499 – 9990 + 501 – 10 + 10000 – 1000 = (499 + 501 – 1000) + (10000 – 9990 – 10) = 0 + 0 = 0

Следовательно, единица является его корнем.

Ответ: 1.

Только усвоенная информация становится знанием. В этом вам помогут онлайн-курсы

Mr. Credo – в белом танце

Функция СТЕПЕНЬ для возведения числа в квадрат

В данном случае для нахождения квадрата числа нам поможет специальная функция под названием СТЕПЕНЬ. Эта функция относится к категории математических операторов и выполняет задачу по возведению указанного числа в заданную степень.

Формула данного оператора выглядит так: =СТЕПЕНЬ(число;степень).

Как мы видим, в данной формуле присутствует два аргумента: число и степень.

• “Число” – аргумент, который может быть представлен двумя способами. Можно прописать конкретное число, которое требуется возвести в степень, либо указать адрес ячейки с требуемым числом.
• “Степень” – аргумент, указывающий степень, в которую будет возводиться наше число. Так как мы рассматриваем возведение числа в квадрат, то указываем значение аргумента, равное цифре 2.

Давайте разберем применение функции СТЕПЕНЬ на примерах:

Способ 1. Указываем в качестве значения аргумента «Число» конкретную цифру

1. Выбираем ячейку, в которой будем производить расчеты. Затем кликаем по кнопке “Вставить функцию” (с левой стороны от строки формул).
2. Откроется окно Мастера функций. Кликаем по текущей категории и выбираем в открывшемся перечне строку “Математические”.
3. Теперь нам нужно в предложенном списке функций найти и кликнуть по оператору  “СТЕПЕНЬ”. Далее подтверждаем действие нажатием OK.
4. Перед нами откроется окно с настройками двух аргументов функции, которое содержит, соответственно, два поля для ввода информации, после заполнения которых жмем кнопку OK.
   • в поле “Число” пишем числовое значение, которое требуется возвести в степень
   • в поле “Степень” указываем нужную нам степень, в нашем случае – 2.
5. В результате проделанных действий мы получим квадрат заданного числа в выбранной ячейке.

Способ 2. Указываем в качестве значения аргумента «Число» адрес ячейки с числом

1. Теперь у нас уже есть конкретное числовое значение в отдельно ячейке (в нашем случае – B3). Так же, как и в первом способе, выделяем ячейку, куда будет выводиться результат, нажимаем на кнопку “Вставить функцию” и выбираем оператор “СТЕПЕНЬ” в категории “Математические”.
2. В отличие от первого способа, теперь вместо указания конкретного числа в поле “Число” указываем адрес ячейки, содержащей нужное число. Для этого кликаем сначала по полю аргумента, затем – по нужной ячейке. Значение поля “Степень” так же равно 2.
3. Далее нажимаем кнопку OK и получаем результат, как и в первом способе, в ячейке с формулой.

Примечание: Также, как и в случае использования формулы для расчета квадрата числа, функцию СТЕПЕНЬ можно применять для возведения числа в любую степень, указав в значении аргумента “Степень” нужную цифру. Например, чтобы возвести число в куб, пишем цифру 3.

Далее жмем Enter и значение куба указанного числа появится ячейке с фукнцией.

Свойства Квадрата Ганна

Ганн в работе использовал квадраты, которые имели начало градусного отсчёта по центру как справа так и слева, а также с левой нижней стороны диагонали образующей квадраты   нечетных чисел. Направление шкалы он использовал как по часовой стрелке, так и против часовой. И наконец, что касается чисел на плоскости квадрата.

Изучение личных работ Ганна показало, что он использовал квадраты в которых числа на плоскости были расположены также как и числа на окружности. Т.е. как против так и по часовой стрелке

Неважно какое направлении в расположении чисел используют, так как результаты от этого не сильно изменяются

Нумерология в основе Квадрата Ганна

Уильям Ганн большое значение придавал нумерологии. Особенно числам упоминаемым в Библии. Это натолкнуло его на мысль о том, что в них заложен некий символизм. Числа – это ключи к зашифрованным знаниям об устройстве вселенной. Так число семь, неоднократно упоминающееся в Библии – семь ангелов, семь дней творения, и такое же число нот в октаве, подсказало идею Ганну в том, что семёрка символизирует как время так и ритм. Важным числом для Ганна было также число 3,5 и не только потому, что оно является половиной семи, но и из-за особой роли отводимой ему в Библии. Христос – дитя, был спрятан в Египте на 3,5 года. Его служение людям продолжалось ровно 3,5 года. Видение Даниила – 42 месяца или 3,5 года.

Либо число двеннадцать, которое у Ганна символизируется с космосом. 12 знаков зодиака и так далее.

Используя эти числа он составлял таблицу магических квадратов с которыми часто сверялся при изменении рыночных цен

Изучая труды великих мудрецов прошлого Ганн не обошел своим вниманием Пифагора, который говорил, что мир построен силою чисел, а это значит, что числа должны быть ключом к пониманию мира. Весьма много предсказаний были и могут быть сделаны именно с помощью чисел

Создание квадрата девяти лишний раз доказывает тот факт, что у Ганна было особое отношение к числам и циклам и всему, что с ними связано.

Ганн не оставил инструкций относительно того как использовать Квадрат девяти. Изучать этот уникальный торговый инструмент каждому из нас приходится самостоятельно. Поэтому в сети интернет можно встретить множество различных версий по его использованию. Ганн говорил, что именно девять чисел мы используем в измерении всего и мы не можем выйти вне этих девяти цифр, не начав повторяться и использовать вновь. Если мы поделим 360 на 9, то получаем 40, что измеряет 40 градусов, 40 месячцев, 40 дней или 40 недель. Это показывает, что основания и вершины биржевых котировок часто выходят в этих углах, измеренных как 1/9 полного круга.

Квадрат разности

Выше мы нашли формулу для суммы одночленов. Давайте теперь найдем формулу для разности, то есть, для \((a-b)^2\):

В более краткой записи имеем:

Квадрат разности: \((a-b)^2=a^2-2ab+b^2\)

Применяется она также, как и предыдущая.

Пример. Упростите выражение \((2a-3)^2-4(a^2-a)\) и найдите его значение при \(a=\frac{17}{8}\).

Решение:

\((2a-3)^2-4(a^2-a)=\)		Если сразу подставить дробь в выражение – придется возводить ее в квадрат и вообще делать объемные вычисления. Попробуем сначала упростить выражение, воспользовавшись формулой выше и раскрыв скобки.
\(=4a^2-12a+9-4a^2+4a=\)		Теперь приведем подобные слагаемые.
\(=-8a+9=\)		Вот теперь подставляем и наслаждаемся простотой вычислений.
\(=-8·\frac{17}{8}+9=-17+9=8\)		Пишем ответ.

Ответ: \(8\).

Вычислительные приёмы

На олимпиаде Кенгуру и на Внешнем независимом тестировании запрещено пользоваться калькуляторами

Поэтому очень важно научиться тратить на вычисления как можно меньше времени, чтобы использовать его на обдумывание задач

Умножение двузначного числа на 11

Чтобы двузначное число умножить на 11, сложите его первую и последнюю цифру. Если результат будет однозначным, впишите его между двумя цифрами первоначального числа, а если двузначным – прибавьте первую цифру результата к первой цифре первоначального числа, а вторую – впишите между цифрами.

Примеры: 45х11

Складываем 4+5=9. Поэтому результатом будет 495.

76х11 Складываем 7+6=13. Единицу прибавляем к семёрке, а тройку пишем в середину и получаем 836.

Математическое обоснование: Пусть нужно двузначное число 10a+b. Умножить на 11. Результатом будет 110a+11b = 100a +10 (a+b) +b

Умножение и деление на 5 и 25

Чтобы число умножить число на 5, его нужно разделить на 2 и умножить на 10. Чтобы число разделить на 5, его нужно умножить на 2 и разделить на 10.

Аналогично, умножение/деление на 25 заменяется делением/умножением на 4 и умножением/делением на 100

Примеры: 36х5

Делим 36 на 2, получаем 18. Умножаем 18 на 10 и получаем 180.

3/5 Умножаем 3 на 2 и получаем 6. Делим 6 на 10 и получаем 0,6

45/25 Умножаем 45 на 4, получаем 180. Делим 180 на 100, получаем 1,8

84х25 Делим 84 на 4, получаем 21. Умножаем 21 на 100 и получаем 2100.

Математическое обоснование: Поскольку 5=10/2, умножение/деление на 2 можно свести к более простым умножениям/делениям на 2 и 10.

Чтобы возвести в квадрат число, оканчивающееся пятёркой, нужно умножить число, полученное отбрасыванием последней пятёрки на следующее в натуральном ряду, и к результату приписать 25.

Примеры: 652 Умножаем 6 на 7, получаем 42. Приписываем 25, получаем 4225.

1152 Умножаем 11 на 12, получаем 132. Приписываем 25, получаем 13225.

Математическое обоснование: Возведём в квадрат число 10n+5. (10n+5)2 = 100n2+100n+25 = 100n(n+1)+25, откуда и следует данное правило.

Возведение в квадрат числа, близкого к круглому

Целесообразно воспользоваться формулами квадрата суммы или разности.

Примеры: 192 = (20-1)2 = 400–40+1=361

422 = (40+2)2 = 1600+160+4 = 1764

Математическое обоснование: Формула квадрата суммы: (a+b)2 = a2+2ab+b2 Формула квадрата разности: (a-b)2 = a2–2ab+b2

Вычитание из степени десятки

Для вычитания числа из степени десятки, нужно последнюю его цифру заменить дополнением до десяти, а остальные (включая первые виртуальные нули) – дополнениями до девяти.

Примеры: 1000-725 = (9-7)(9-2)(10-5) = 275

100000 – 1237 = 100000 – 01237 = (9-0)(9-1)(9-2)(9-3)(10-7) = 98763

Математическое обоснование: Правило следует из алгоритма вычитания столбиком.

Прибавление числа, близкого к степени десятки

Вместо прибавления числа, состоящего из девяток и оканчивающегося на 9 (8, 7, 6 и т.д.), прибавьте следующую большую степень десятки и вычтите 1 (2, 3, 4 и.т.д)

Примеры: 125+999 = 1125-1 = 1124

6528+996 =7258-4=7254

Математическое обоснование: Для k-значного числа 99…9 = 100..00 – 1

Упрощённые признаки делимости на 4 и 8

Обычно для проверки делимости на 4 применяется следующий признак: Если двуциферное окончание числа делится на 4, то и само число делится на 4.

Однако, использовав обобщённый признак делимости, заметим, что число 10 даёт остаток 2 при делении на 4. Поэтому переформулируем правило так: Если сумма последней цифры с удвоенной предпоследней делится на 4, то и само число делится на 4.

Аналогично для делимости на 8. Вместо проверки на делимость трёхциферного окончания, можно выполнять проверку суммы последней, удвоенной предпоследней и учетверённой третьей с конца цифры.

Примеры: Число 1324 4+2*2=8 – делится на 4.

4+2*2+3*4=20 – не делится на 8

Число 6328 8+2*2=12 – делится на 4.

8+2*2+3*4=24 – делится на 8

Математическое обоснование: Обобщённый признак делимости подробно рассмотрен в отдельной статье.

Возведение трёхчлена в степень

Трёхчлен — это многочлен, состоящий из трёх членов. Например, выражение a + b + c является трёхчленом.

Иногда может возникнуть задача возвести трёхчлен в степень. Например, возведём в квадрат трехчлен a + b + c

(a + b + c)2

Два члена внутри скобок можно заключить в скобки. К примеру, заключим сумму a + b в скобки:

((a + b) + c)2

В этом случае сумма a + b будет рассматриваться как один член. Тогда получается, что в квадрат мы возводим не трёхчлен, а двучлен. Сумма a + b будет первым членом, а член c — вторым членом. А как возводить в квадрат двучлен мы уже знаем. Для этого можно воспользоваться формулой квадрата суммы двух выражений:

(a + b)2 = a2 + 2ab + b2

Применим эту формулу к нашему примеру:

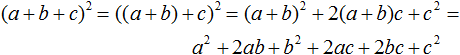
Таким же способом можно возвести в квадрат многочлен, состоящий из четырёх и более членов. Например, возведем в квадрат многочлен a + b + c + d

(a + b + c + d)2

Представим многочлен в виде суммы двух выражений: a + b и c + d. Для этого заключим их в скобки:

((a + b) + (c + d))2

Теперь воспользуемся формулой квадрата суммы двух выражений:

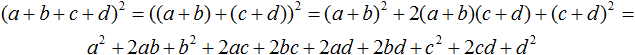
Свойства степеней:

Произведение степеней. При умножении степеней с одинаковыми основаниями основание остаётся без изменений, а показатели степеней складываются.

am · an = am + n

62 · 64 = 62+4 = 66

Частное степеней. При делении степеней с одинаковыми основаниями основание остаётся без изменений, а из показателя степени делимого вычитают показатель степени делителя.

am / an = am – n

64 / 62 = 64 – 2 = 62

Возведение степени в степень. При возведении степени в степень основание степени остаётся без изменения, а показатели степеней перемножаются.

(an) m = an · m

(64)6 = 64 · 6 = 624

Степень произведения. При возведении в степень произведения каждый из множителей возводится в степень. Затем полученные результаты перемножаются.

(a · b)n = an · bn

(6 · 6)3 = 63 · 63

Степень частного (дроби). Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель, и первый результат разделить на второй. При возведении в степень дроби нужно возвести в степень и числитель, и знаменатель.

(a / b)n = an / bn

(6 / 6)3 = 63 / 63

Примечание:  Фото https://www.pexels.com, https://pixabay.com

карта сайта

Коэффициент востребованности
60

Гармоничные отношения это. Залог гармонии в отношениях

Каждый мужчина желает быть главным во всем: в работе, в дружбе, в семье

Ориентированному на результат карьеристу важно добиться успеха и занимать высокий пост в фирме, где он осуществляет свою трудовую деятельность. Любителю приключений и душе компании важно сохранять лидерство среди своих друзей

А примерному семьянину просто необходимо быть главой и опорой семьи. Равно как и женщины: далеко не каждая готова смиренно подчиняться воле оппонента.

Современное общество любит и привыкло видеть целеустремленных и сильных духом, волевых дам. Вот именно на почве такого стремления к первенству, желания быть лучше и сильнее других, попыток превзойти не только своего соперника, но и ближнего, люди приходят к полному отсутствию гармонии в отношениях между мужчиной и женщиной.

Когда каждый тянет одеяло на себя, когда никто в паре не способен поступиться своими принципами. Тогда о налаженном контакте и благоприятном микроклимате в отношениях между двумя говорить нельзя. Лишь обоюдные усилия в достижении общего знаменателя способны привести к слаженности и положительной динамике в притирании молодых людей друг к другу. Залог гармоничных отношений между мужчиной и женщиной – это понимание ими весомости и значимости не только своего собственного «я», но и роли партнера в своей жизни.

Как пользоваться инженерным калькулятором – на примерах

Как возвести в степень

Чтобы возвести, к примеру, 12^3 вводите в следующей последовательности:

12 3

12, клавиша «икс в степени игрик» , 3, знак равенства

Ответ: 1728

Как найти корень кубический

Допустим, что мы извлекаем корень кубический из 729, нажмите в таком порядке:

729

729, «кубический корень из икс», равенства

Как найти корень на калькуляторе

Задача: Найти квадратный корень 36.

Решение: всё просто, нажимаем так:

36 y√x] 2

36, «корень из икса, в степени игрик», нужную нам степень 2, равно

Ответ: 6

При помощи этой функции вы можете найти корень в любой степени, не только квадратный.

Как возвести в квадрат

Для возведения в квадрат онлайн вычислительная программа содержит две функции:

«икс в степени игрик», «икс в квадрате»

Последовательность ввода данных такая же, как и раньше – сначала исходную величину, затем «x^2» и знак равно, либо если не квадрат, а произвольное число, необходимо нажать функцию «x^y», затем указать необходимую степень и так же нажать знак «равно».

Например: 45 6

Ответ: сорок пять в шестой степ. равно 8303765625