Закон парето: как достигать поставленных целей с минимальными затратами

Содержание

Пример? Ну вот, смотрите

Представим себе кино про группу диверсантов во вражеском тылу. Если группа собрана правильно и фильм не сделан по комиксам про универсальных солдат-суперменов, то умения членов группы неоднородны.

Давайте для удобства нарисуем таблицу.

	Стрельба	Ближний бой	Минирование	Знание языков	Компьютер
Джон	5	3	4	2	3
Джейн	4	2	4	5	4
Карл	2	4	5	3	3
Джим	3	5	3	4	3
Том	4	4	2	4	5
Сумма баллов	18	18	18	18	18

Если проанализировать любой параметр отдельно (стрельба, ближний бой и т.д) «по Парето», можно увидеть, что состав группы не оптимален. И есть «лишние люди». Но если смотреть на группу в целом, мы видим, что по любому параметру достигается максимум. И максимумы достигаются на разных людях.
Чтобы было еще нагляднее, попробуем оптимизировать «по Парето», например, параметр «Стрельба». Убираем двух «аутсайдеров», Карла и Джима.

	Стрельба	Ближний бой	Минирование	Знание языков	Компьютер
Джон	5	3	4	2	3
Джейн	4	2	4	5	4
Том	4	4	2	4	5
Сумма баллов	13	9	10	11	12

Теперь группа сможет неплохо пострелять или взломать сервер. Но не факт, что отобьется от толпы разгневанных сисадминов.

Получается, когда Парето говорил о том, что неравномерность распределения доходов неизбежна — он был умнее своих последователей. Неравномерность — следствие того, что мы имеем дело со сложной системой.

И вряд ли Вильфредо Парето ожидал, что из его локального наблюдения о распределении доходов потомки попытаются сделать столь далеко идущие выводы.

Не надо так.

Иллюстрация к тексту — промо к фильму «Бесславные ублюдки».

Теория элит Вильфредо Парето

Большинство людей знает ученого именно благодаря этой теории. По его мнению, элиты постоянно сменяют друг друга, а история является «кладбищем элит». Таким образом, основные причины политических изменений Вильфредо Парето видел в циркуляции элит. Для элит, как отмечает Парето, характерна тенденция к упадку. «Неэлиты», в свою очередь, могут создавать для них вполне достойных преемников

И это очень важно, ведь дети, как правило, не обладают теми выдающимися особенностями, которые были у их родителей. Элиты должны постоянно сменяться, так как стоящие у власти люди со временем теряют ту энергию, которая помогла им завоевать высокий пост

Общество непрерывно стремится к социальному равенству, которое достигается грамотным взаимодействием четырех важнейших сил, которые Парето назвал элементами. Элементы, по его мнению, могут быть: социальными, экономическими, политическими и интеллектуальными.

Как использовать принцип Парето для повышения эффективности работы компании

Несмотря на изменчивость границ данного принципа, даже значение 65:35 принесет грамотному руководителю выгоду. Для этого необходимо детально ознакомиться с процессом изготовления товара, его сбыта и выявить их слабые места.

Также для повышения эффективности используют основы грамотного тайм-менеджмента: 80% сотрудников должны обратить свое внимание на 20% клиентов, которые приносят 80% прибыли. В это же время, 20% сотрудников, которые приносят 80% прибыли, должны заниматься поиском новых клиентов или модернизацией производства, расширением ассортимента и т.д

Важно

Большую выгоду приносит работа с ассортиментом, его изменения и дополнения, нежели упорная и самоотверженная работа сотрудников.

Чтобы увеличить продажи, необходима серьезная работа аналитика. Нужно изучить рынок, понять, какие товары пользуются наибольшим спросом, на какие рынки сбыта уместно поставлять производимый товар и т.д. Это позволит определить те самые 20% товара, который приносит 80% прибыли. Затем менеджеры должны приложить свои усилия для сбыта этих 20%.

Кроме этого, повысить эффективность работы компании можно за счет обучения каждого отдельного сотрудника тайм-менеджменту. В условиях, когда каждый работник сосредоточится на делах, приносящих ему 80% выгоды, его личная выработка и производительность компании в целом вырастут.

Свойства

Моменты и характерная функция

Ожидаемое значение из случайной величины после распределения Парето

E⁡(Икс)знак равно{∞α≤1,αИксмα-1α>1.{\ displaystyle \ operatorname {E} (X) = {\ begin {case} \ infty & \ alpha \ leq 1, \\ {\ frac {\ alpha x _ {\ mathrm {m}}} {\ alpha -1} } & \ alpha> 1. \ end {case}}}

Дисперсия из случайной величины после распределения Парето

Вар⁡(Икс)знак равно{∞α∈(1,2,(Иксмα-1)2αα-2α>2.{\ displaystyle \ operatorname {Var} (X) = {\ begin {cases} \ infty & \ alpha \ in (1,2], \\\ left ({\ frac {x _ {\ mathrm {m}}} { \ alpha -1}} \ right) ^ {2} {\ frac {\ alpha} {\ alpha -2}} & \ alpha> 2. \ end {ases}}}

(Если α ≤ 1, дисперсия не существует.)

Сырьевые моменты являются

μп′знак равно{∞α≤п,αИксмпα-пα>п.{\ displaystyle \ mu _ {n} ‘= {\ begin {case} \ infty & \ alpha \ leq n, \\ {\ frac {\ alpha x _ {\ mathrm {m}} ^ {n}} {\ alpha -n}} & \ alpha> n. \ end {case}}}

Функция, производящая момент, определяется только для неположительных значений t  ≤ 0 как

M(т;α,Иксм)знак равноE⁡етИксзнак равноα(-Иксмт)αΓ(-α,-Иксмт){\ displaystyle M \ left (t; \ alpha, x _ {\ mathrm {m}} \ right) = \ operatorname {E} \ left = \ alpha (-x _ {\ mathrm { m}} t) ^ {\ alpha} \ Gamma (- \ alpha, -x _ {\ mathrm {m}} t)}

M(,α,Иксм)знак равно1.{\ displaystyle M \ left (0, \ alpha, x _ {\ mathrm {m}} \ right) = 1.}

Характеристическая функция задается

φ(т;α,Иксм)знак равноα(-яИксмт)αΓ(-α,-яИксмт),{\ displaystyle \ varphi (t; \ alpha, x _ {\ mathrm {m}}) = \ alpha (-ix _ {\ mathrm {m}} t) ^ {\ alpha} \ Gamma (- \ alpha, -ix_ { \ mathrm {m}} t),}

где Γ ( a ,  x ) — неполная гамма-функция .

Параметры могут быть решены методом моментов .

Условные распределения

Условное распределение вероятностей из Парето- распределенной случайной величины, учитывая событие , которое оно больше или равно определенный номер  превышения , является распределение Парето с тем же индексом паретовского  , но с минимумом  вместо .
Икс1{\ displaystyle x_ {1}}Иксм{\ displaystyle x _ {\ text {m}}}α{\ displaystyle \ alpha}Икс1{\ displaystyle x_ {1}}Иксм{\ displaystyle x _ {\ text {m}}}

Характеризационная теорема

Предположим, что это независимые одинаково распределенные случайные величины , распределение вероятностей которых поддерживается на интервале для некоторых . Предположим, что для всех две случайные величины и независимы. Тогда обычное распределение — это распределение Парето.
Икс1,Икс2,Икс3,…{\ Displaystyle X_ {1}, X_ {2}, X_ {3}, \ dotsc} Иксм,∞){\ Displaystyle [х _ {\ текст {м}}, \ infty)}Иксм>{\ displaystyle x _ {\ text {m}}> 0}п{\ displaystyle n}мин{Икс1,…,Иксп}{\ displaystyle \ min \ {X_ {1}, \ dotsc, X_ {n} \}}(Икс1+⋯+Иксп)мин{Икс1,…,Иксп}{\ displaystyle (X_ {1} + \ dotsb + X_ {n}) / \ min \ {X_ {1}, \ dotsc, X_ {n} \}}

Среднее геометрическое

Геометрическое среднее ( G ) является

гзнак равноИксмexp⁡(1α).{\ displaystyle G = x _ {\ text {m}} \ exp \ left ({\ frac {1} {\ alpha}} \ right).}

Гармоническое среднее

Гармоническое среднее ( Н ) является

ЧАСзнак равноИксм(1+1α).{\ displaystyle H = x _ {\ text {m}} \ left (1 + {\ frac {1} {\ alpha}} \ right).}

Графическое представление

Характерное криволинейное распределение с « длинным хвостом » при построении в линейном масштабе маскирует лежащую в основе простоту функции при нанесении на логарифмический график , который затем принимает форму прямой линии с отрицательным градиентом: это следует из формулы для функция плотности вероятности, что для x ≥ x _m ,

журнал⁡жИкс(Икс)знак равножурнал⁡(αИксмαИксα+1)знак равножурнал⁡(αИксмα)-(α+1)журнал⁡Икс.{\ displaystyle \ log f_ {X} (x) = \ log \ left (\ alpha {\ frac {x _ {\ mathrm {m}} ^ {\ alpha}} {x ^ {\ alpha +1}}} \ справа) = \ log (\ alpha x _ {\ mathrm {m}} ^ {\ alpha}) — (\ alpha +1) \ log x.}

Поскольку α положительно, градиент — ( α  + 1) отрицательный.

Актуальность экономического закона

Большинство из нас считают, что все жизненные факторы имеют равноценное влияние на конечный результат. Те лица, которые пренебрегают правилом Парето, искренне думают, что все затрачиваемые усилия приносят одинаковый результат, а все клиенты одинаковую прибыль для магазина.

То же самое можно предположить и о круге общения или же о равноценности уровня образования, независимо от места учебы. Но все это ошибочные суждения.

Анализируя принцип 20/80 можно прийти к выводу, что небольшое количество действий является причиной завершенного конечного результата. Такое правило существенно повлияло на развитие многих известных корпораций, таких как IBM, Apple, а также поспособствовало достижению успеха многих бизнесменов, инвесторов и изобретателей.

Закон Парето, или: как работает правило 20/80

Итальянский социолог и экономист Вильфредо Парето в последние годы XIX века проводил достаточно любопытные исследования. Он анализировал, в каком соотношении распределяется капитал между различными слоями населения на территории Англии. Ученый сделал ошеломляющее открытие: меньшинству населения, а именно 20 %, принадлежит большая часть богатства страны, точнее 80 %. Более глубокие исследования подтвердили этот факт.

Принцип 20/80 применяют для достижения максимальных результатов, затрачивая при этом меньшие усилия.

Общий смысл правила в следующем: при достижении какой-либо цели из 100 % приложенных усилий всего 20 % дают 80 % результата. Если совсем упростить, то 20-ти процентам на входе соответствует 80 процентов на выходе.

Правило также работает в обратном порядке: затратив 80 % чего-либо, можно получить только 20% того, к чему стремился человек.

Иными словами, необходимо концентрироваться на таких действиях, которые являются наиболее результативными. От малоэффективных усилий нужно избавляться. За счет экономии времени, сил и финансов повысится продуктивность любой деятельности, а значит, и жизнь человека улучшится.

Правило 20/80 работает во всех аспектах жизни каждого человека и человечества в целом.

Этот факт доказан последователями Парето. Вот всего несколько примеров…

• Из всего объема прочитанной литературы лишь 20 % дают людям 80 % полезных знаний.
• Только 20 % из общего количества сайтов обладают интернет-трафиком в объеме 80 %.
• Всего 20 % населения земного шара являются владельцами 80-ти процентов мировых финансов и ресурсов (это, кстати, самый популярный пример).

Детальный анализ причин и следствий различных событий приводит к вполне определенному заключению: меньшие усилия в большей степени влияют на хорошую результативность. Остальная активность почти не приносит пользы.

Хондромаляция коленного сустава что это такое, как лечить?

Возможности использования в повседневной жизни

Применять правило Парето можно практически в любой жизненной ситуации, достаточно помнить следующие правила:

1. В любой деятельности следует выявить 20% действий, способных дать большую часть результата. То есть, выполняя работу, определяйте вначале наиболее важные процессы и выполняйте их, только потом переходите к «шлифовке» и доработке полученного результата.
2. Нужно брать на себя только те обязанности, которые можно выполнять с максимальной эффективностью (то есть делать 80% работы при 20% своих усилий). Это позволяет уменьшить рабочую нагрузку и направить освободившееся время и силы в другое русло.
3. Вместо того, чтобы довести до конца одно дело, можно «почти закончить» несколько дел, затрачивая аналогичное количество времени и сил. Работает только там, где «почти закончить» приемлемая стадия завершения результата, то есть не требуется качественная работа над мелкими деталями.
4. Принцип хорошо работает только там, где нужно количество, а не качество. При работе со сложными задачами, требующими внимания ко всем деталям лучше от него отказаться. Закон Парето, к примеру, не применим к часовщику, ведь завершенный на 80% механизм не будет должным образом работать, законченное на 80% лечение не гарантирует избавление от болезни и т.д.

Материалы по теме «Разработки, исследования»

Китайская и японская философия жизни

Мудрость Поднебесной можно обозначить как науку бодрствования духа и чуткого понимания текущего момента. Интересны китайские мудрости о жизни, они стремятся разделить бытие на внутреннее и внешнее. Страна издавна славилась огромным количеством философов. Великая китайская мудрость – цитаты о жизни.

• Если сделал что-то хорошее — никогда не жалей. Жалеть нужно только о том, что сделал плохо.
• Искусство жизни заключается в том, чтобы быть здоровым настолько и так долго, насколько сможешь, и довольствоваться тем, что уже есть в наличии.
• Волею судьбы человек может временно править миром, а благодаря силе любви он сможет править вечно.

Японская мудрость заключается в постоянном совершенствовании души, в гармонии взаимоотношений мира с человеком. Самураи стремятся найти красоту повсюду – во всем окружающем. Японцы считают мудрость сокровищем для последующих поколений. Философия их направлена на духовный мир человека, его внутреннее «Я» и окружающий мир. На жизненные знания, умение ими пользоваться и применять в быту. Об этом говорят японские мудрости о жизни.

• Если будет все в жизни так, как хочется тебе, то жизнь станет просто неинтересной.
• Даже если у тебя совсем ничего нет, это неправда – у тебя есть жизнь, в которой есть абсолютно все!
• Лучше быть для хорошего человека врагом, чем для плохого – другом.

История

Вильфредо Парето

Как универсальный принцип предложен Джозефом Джураном, который в своей публикации сослался на частную закономерность, выявленную итальянским экономистом и социологом Вильфредо Парето в 1897 году. Идею принципа Парето Джуран изложил в первом издании своего справочника по качеству в 1951 году. Впоследствии в статье «Mea culpa» Джуран рассказал, как он пришел к этой идее, и почему возникло название «принцип Парето», хотя сам Парето никакого принципа не предлагал. В. Парето исследовал конкретные кумулятивные зависимости распределения доходов населения в Италии, которые графически описываются кривой Лоренца, поскольку именно такая зависимость была предложена американским экономистом Максом Отто Лоренцем в 1905 году. По сути, принцип Парето отражает неравномерность распределения причин и следствий в природе. Другим известным показателем степени неравномерности кумулятивного распределения является коэффициент Джини, предложенный итальянским экономистом и социологом Коррадо Джини в 1912 году.

Соблюдение принципа 80/20 очень часто встречается в самых разных областях. Например, во многие времена во многих сообществах оказывалось, что 20 % людей обладают 80 % капитала, в бизнесе зачастую 20 % покупателей или постоянных клиентов приносят 80 % прибыли. Но в этих утверждениях фундаментальными являются не приведённые числовые значения, а сам факт их существенного различия, конкретные цифры степени неравномерности могут быть любыми.

Последние годы

В начале 1920-х итальянский социолог опубликовал несколько важнейших работ. В 1921 году вышла книга Парето Вильфредо «Трансформация демократии». В ней ученый в обобщенном виде раскрыл все свои основные идеи. В нескольких своих трудах, Парето выказывал сочувствие итальянскому фашизму, приверженцем идеологии которого являлся. Именно в эти годы, к власти в Италии пришел Б. Муссолини. Новое правительство уважало Парето, а некоторые его члены даже считали себя учениками социолога. В результате в 1923 году Вильфредо стал сенатором Итальянского королевства. Вскоре он умер и был похоронен в Селиньи.

Как поднять уровень тестостерона

Что такое закон Парето?

<?php if ( ! is_single ( array(883, 15772, 33900, 37506) ) ) { ?><?php } ?>
Как вы уже наверняка поняли из информации об истории возникновения этого термина, закон Парето – это эмпирическое правило, в основе которого лежит соотношение цифр 80% к 20%.

Четкого обозначения этого закона нет, поскольку его применяют для различных сфер деятельности.

Но, если говорить в общем, то можно его сформулировать приблизительно так: 20% наших усилий дают 80% желанного результата и наоборот: 80% усилий оборачиваются лишь реализацией 20% желаний.

То есть, для того, чтобы не стучаться в закрытую дверь, нужно выбирать наиболее важные цели, реализовать которые можно с минимальными затратами.

Если смотреть глубже, то закон Парето – пропорциональное соотношение между действиями (причинами) и результатами, то есть – последствиями.

Конечно, нельзя сказать, что соотношений 20 к 80 является универсальным и применимо везде, пропорции могут быть немного другими.

Но, поскольку детальный анализ каждый раз проводить никто не будет, то принято считать пропорциональное соотношение, выведенное Вильфредо, наиболее оптимальным.

Основные правила закона Парето:

• большинство наших ежедневных действий – неэффективны и попросту воруют наше время;
• важных факторов, формирующих успех, не так уж и много;
• то, что мы видим, не всегда является таким в действительности, нужно учитывать нюансы;
• нужно на начальном этапе уметь видеть, работает ваша идея или нет, если нет, то думать, что можно изменить;
• как бы сильно мы не старались, в большинстве своем эти усилия неэффективны.

Недостаток

Понимая, что только 20% действий принесет необходимый результат, человек все равно вынужден затрачивать остальные 80% усилий. Иначе организовать работу не получится. Например, заказчик нуждается только в некоторой части продукции, производством которой занимается предприниматель. Однако его вряд ли обрадует, если поставщик начнет производить только этот процент. Ему необходимо из чего-то выбирать. И такая логика прослеживается в любой сфере деятельности.

Принцип Парето простыми словами

Если говорить просто и понятно, то закон Парето подразумевает получение наиболее максимального результата при наименьших на это затратах. Другими словами, при затрате всего 20% усилий или средств, мы можем получить 80% положительного результата.

Такая схема очень проста и демонстрирует то, что вкладывая как физическую силу, так и денежные средства или время, можно без проблем достичь хороших показателей. По сути, принцип Парето можно применять не только к экономике и менеджменту, а и в повседневной жизни и в быту.

Важно выделить тот факт, что значения 80/20 условные, ведь показатели могут быть:

• 70/30;
• 90/10;
• 75/25.

Правило 20% на 80% — это обобщенный показатель затрат и выгоды. Он дает понять, что максимум эффективности можно ожидать, только в случае использования самых оптимальных и наиболее подходящих ресурсов, обладающих хорошей результативностью.

Биография

Вильфредо Парето родился 15 июля  г. в Париже в семье итальянского маркиза, выходца из портового города Генуя, вынужденного эмигрировать из-за своих либеральных и республиканских убеждений. Мать Парето была француженкой, и он с детства одинаково хорошо владел итальянским и французским, однако всю жизнь он ощущал себя прежде всего итальянцем.

В 1858 году семья Парето вернулась в Италию. Там Вильфредо начинает учиться и получает одновременно классическое, гуманитарное и техническое образование

При этом большое внимание он уделяет изучению математики.

После окончания Политехнической школы в Турине Парето в  г. защищает диссертацию «Фундаментальные принципы равновесия в твёрдых телах»

Тема эта воспринимается как предзнаменование, учитывая важное место понятия равновесия в его последующих экономических и социологических трудах. В течение ряда лет он занимал довольно важные должности в железнодорожном ведомстве и в металлургической компании.

В 1890-е годы он предпринимает неудачную попытку заняться политической деятельностью. В это же время он активно занимается публицистикой, чтением и переводами классических текстов. В первой половине 90-х годов Парето публикует ряд исследований в области экономической теории и математической экономики. С  г. и до конца жизни он был профессором политической экономии Лозаннского университета в Швейцарии, сменив в этой должности известного экономиста Леона Вальраса.

В последний год жизни Парето в Италии уже установился фашистский режим. Некоторые видные деятели этого режима, и прежде всего сам Муссолини, считали себя учениками лозаннского профессора. В связи с этим в  г. он был удостоен звания сенатора Италии. Парето выразил сдержанную поддержку новому режиму, одновременно призвав его быть либеральным и не ограничивать академических свобод.

Умер Парето 20 августа  г. в Селиньи (Швейцария), где он жил последние годы своей жизни; там он и был похоронен.

Определите «центральный узел»

Когда вы составите список действий и увидите сколько тратите времени на каждое, вы поймёте, правильно ли расходуете свои часы. Предположим, есть задача заработать в этом месяце больше, чем в прошлом. Для её достижения нужно «расчертить» свой рабочий день. Посмотрите сколько времени вы отводите на коммуникацию с клиентами, сколько на сбор информации для профессионального развития и сколько на просмотр социальных сетей и совещания с коллегами

Уже на этом этапе можно выявить «важное» и, ради цели, отказаться от Instagram и Facebook

Рассмотрите каждое из этих действий глубже. Если вы видите, что большая часть времени, которая уходит на контакт с напарниками даёт только 20% профессионального результата, то вам нужно сократить участие в таких переговорах. Сместите фокус общения в сторону только рабочих тем и тех сотрудников, которые помогут добиться большего.

То же самое касается клиентов. Согласно правилу, 2 из 10 заказчиков дадут 80% результата. Определите, с кем из них сможете заработать больше и сосредоточьтесь на общении с ними.

С ходом времени приоритеты смещаются. Поэтому периодически пересматривайте список и выявляйте новые «центральные узлы».

Ссылки

Принцип Парето в продажах

Правило Парето в продажах является одним из основополагающих. Любой бизнесмен, топ-менеджер по продажам стараются выявить эффективные составляющие 20% действий, условий, партнеров, товаров, которые позволят совершать сделки, продажи на максимальном уровне. Успешные предприниматели выявили следующие закономерности по Парето:

• 20% времени потраченное на управление бизнесом – 80% результативной деятельности;
• 80% продаж обеспечивают лишь 20% менеджеров или продавцов;
• Из всей линейки ассортимента товаров только 20% приносят стабильный 80% доход;
• Постоянные клиенты или покупатели, это те 20% приносящие 80% доход фирме или производству.

Обзор

« Оптимальность по Парето» — это формально определенное понятие, используемое для описания оптимального распределения . Распределение не является оптимальным по Парето, если существует альтернативное распределение, при котором можно улучшить благосостояние по крайней мере одного участника без снижения благосостояния любого другого участника. Если есть передача, которая удовлетворяет этому условию, перераспределение называется «улучшением Парето». Когда дальнейшие улучшения Парето невозможны, распределение является «оптимальным по Парето».

Формальное представление концепции в экономике выглядит следующим образом. Рассмотрим экономику с агентами и товарами. Тогда распределение , в котором для всех I , является оптимальным по Парето , если не существует никакого другого достижимое распределение такое , что для функции полезности для каждого агента , для всех с для некоторых . Здесь, в этой простой экономике, «осуществимость» относится к распределению, при котором общая сумма каждого выделенного товара не превышает общую сумму товара в экономике. В более сложной экономике с производством распределение будет состоять как из векторов потребления, так и из векторов производства, и осуществимость потребует, чтобы общее количество каждого потребляемого товара не превышало первоначального запаса плюс произведенное количество.
п{\ displaystyle n}k{\ displaystyle k}{Икс1,…,Иксп}{\ Displaystyle \ {х_ {1}, …, х_ {п} \}}Икся∈рk{\ displaystyle x_ {i} \ in \ mathbb {R} ^ {k}}{Икс1′,…,Иксп′}{\ Displaystyle \ {x_ {1} ‘, …, x_ {n}’ \}}тыя{\ displaystyle u_ {i}}я{\ displaystyle i}тыя(Икся′)≥тыя(Икся){\ Displaystyle и_ {я} (х_ {я} ‘) \ geq и_ {я} (х_ {я})}я∈{1,…,п}{\ Displaystyle я \ в \ {1, …, п \}}тыя(Икся′)>тыя(Икся){\ displaystyle u_ {i} (x_ {i} ‘)> u_ {i} (x_ {i})}я{\ displaystyle i}

В принципе, переход от обычно неэффективного экономического распределения к эффективному не обязательно считается улучшением по Парето. Даже при общем выигрыше в экономике, если перераспределение ставит в невыгодное положение отдельный агент, распределение не является оптимальным по Парето. Например, если изменение экономической политики устраняет монополию и этот рынок впоследствии становится конкурентным, выгода для других может быть большой. Однако, поскольку монополист находится в невыгодном положении, это не улучшение по Парето. Теоретически, если выгода для экономики больше, чем убыток для монополиста, монополист может получить компенсацию за свои убытки, при этом оставив чистую прибыль другим участникам экономики, допуская улучшение по Парето. Таким образом, на практике, чтобы гарантировать, что изменения, направленные на достижение эффективности по Парето, никого не ставят в невыгодное положение, может потребоваться компенсация одной или нескольких сторон. В реальном мире признается, что такие компенсации могут иметь непредвиденные последствия, приводящие к искажениям стимулов с течением времени, поскольку агенты предположительно ожидают таких компенсаций и соответственно изменяют свои действия.

В идеализированных условиях первой теоремы благосостояния система свободных рынков , также называемая « конкурентным равновесием », приводит к результату, эффективному по Парето. Впервые математически это продемонстрировали экономисты Кеннет Эрроу и Жерар Дебре .

Однако результат верен только при ограничительных предположениях, необходимых для доказательства: рынки существуют для всех возможных товаров, поэтому внешние эффекты отсутствуют ; все рынки находятся в полном равновесии; рынки совершенно конкурентны; транзакционные издержки незначительны; и участники рынка обладают прекрасной информацией .

В отсутствие точной информации или полных рынков результаты, как правило, будут неэффективными по Парето, согласно .

Вторая теорема благосостояния , по существу , противоположна первой благосостояния-теоремы. В нем говорится, что при аналогичных идеальных допущениях любой оптимум Парето может быть получен с помощью некоторого конкурентного равновесия или системы свободного рынка , хотя для этого также может потребоваться единовременная передача богатства.

Тренировка в стиле Cardicore. Что это такое?

Навигация

Суть закона Парето

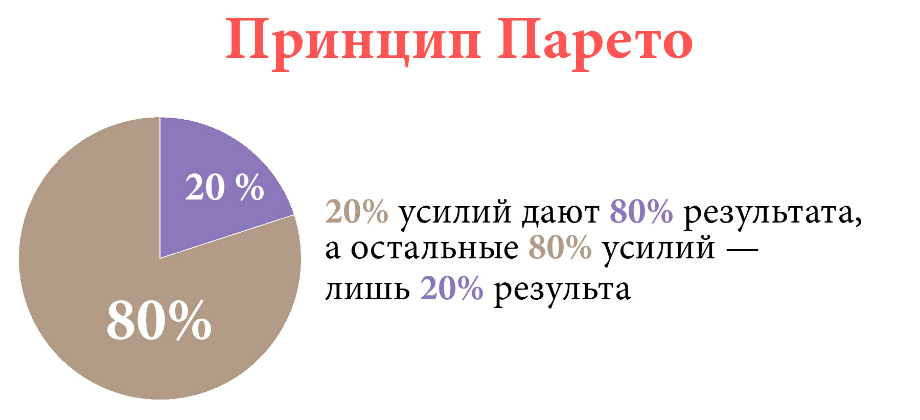
Как вы уже поняли, суть закона Парето заключается в том, что лишь малая часть всех ваших действий, а именно лишь 20%, приводит к наибольшим результатам, то есть 80% успеха в любом деле. И наоборот – большая часть ваших усилий (остальные 80%) приводит к весьма скромным достижениям (20% результатов).

Конечно, это несколько условные показатели. На практике может оказаться, что значения 20 к 80 могут несколько колебаться в одну или же другую сторону. К примеру, если отнести принцип Парето к вашей работе, то большую часть результатов могут давать 35 или даже 10% всех затрачиваемых усилий. Однако какими бы ни были эти показатели, сама суть закона всегда сохраняется. То есть вам нужно подобрать самые благоприятные условия, выбрать необходимые ресурсы и определиться с конкретными способами достижения, которые и приносят большую часть успеха в любом деле.

Многие люди ошибочно считают, что абсолютно все действия в нашей жизни одинаково влияют на изменение или же сохранение текущего положения. Но теперь вы понимаете, что это далеко не так

Те, кто не имеет понятия о принципе Парето или же просто не использует его, уделяют одинаковое внимание всем клиентам, даже если некоторые из них попросту отбирают время. Считают, что все их знакомые и друзья важны в равной степени, и даже выбирая учебное заведение полагают, что полученные там знания будут такими же, как и в остальных схожих ВУЗах

Но если провести внимательный анализ причинно-следственных связей наших действий, то окажется, что лишь меньшая часть конкретных усилий и привела нас к ожидаемому результату. В то же время значительная часть времени была просто потеряна зря. Но прежде чем перейти к более детальным примерам и практическим рекомендациям, давайте рассмотрим историю возникновения принципа Парето.

Использование в технике

Понятие эффективности Парето использовалось в технике. Учитывая множество вариантов и способ оценки их, граница Парето или множество Парето или парето фронт есть множество вариантов , которые являются эффективными по Парето

Ограничивая внимание набором вариантов, которые эффективны по Парето, разработчик может пойти на компромиссы в рамках этого набора, вместо того чтобы рассматривать полный диапазон каждого параметра.

Пример границы Парето. Пунктирные точки представляют собой возможные варианты, меньшие значения предпочтительнее, чем большие. Точка C не на границе Парето , поскольку она доминирует как точки А и точкой Б . Точки A и B не находятся под строгим преобладанием каких-либо других и, следовательно, лежат на границе.

Производственные возможности границы . Красная линия является примером границы, эффективной по Парето, где граница и область слева и ниже представляют собой непрерывный набор вариантов. Красные точки на границе — примеры оптимального по Парето выбора производства. Точки за пределами границы, такие как N и K, не являются эффективными по Парето, поскольку существуют точки на границе, которые доминируют над ними.

Граница Парето

Для данной системы граница Парето или множество Парето — это набор параметризаций (распределений), которые все являются эффективными по Парето. Определение границ Парето особенно полезно в инженерии. Предлагая все потенциально оптимальные решения, разработчик может идти на компромисс в рамках этого ограниченного набора параметров, вместо того, чтобы учитывать все диапазоны параметров.

Границу Парето, P ( Y ), можно более формально описать следующим образом. Рассмотрим систему с функцией , где X — это компактное множество допустимых решений в метрическом пространстве , а Y — допустимое множество критериальных векторов в , такое что .
жрп→рм{\ displaystyle f: \ mathbb {R} ^ {n} \ rightarrow \ mathbb {R} ^ {m}} рп{\ Displaystyle \ mathbb {R} ^ {п}}рм{\ Displaystyle \ mathbb {R} ^ {m}}Yзнак равно{y∈рмyзнак равнож(Икс),Икс∈Икс}{\ Displaystyle Y = \ {Y \ in \ mathbb {R} ^ {m}: \; y = f (x), x \ in X \; \}}

Мы предполагаем, что известны предпочтительные направления значений критериев. Точка предпочтительнее (строго доминирует) над другой точкой , записанной как . Граница Парето, таким образом, записывается как:
y′′∈рм{\ Displaystyle у ^ {\ прайм \ прайм} \ в \ mathbb {R} ^ {м}}y′∈рм{\ displaystyle y ^ {\ prime} \ in \ mathbb {R} ^ {m}}y′′≻y′{\ Displaystyle у ^ {\ прайм \ прайм} \ сук у ^ {\ прайм}}

п(Y)знак равно{y′∈Y{y′′∈Yy′′≻y′,y′≠y′′}знак равно∅}.{\ Displaystyle P (Y) = \ {y ^ {\ prime} \ in Y: \; \ {y ^ {\ prime \ prime} \ in Y: \; y ^ {\ prime \ prime} \ succ y ^ {\ prime}, y ^ {\ prime} \ neq y ^ {\ prime \ prime} \; \} = \ emptyset \}.}

Предельная ставка замещения

Важным аспектом границы Парето в экономике является то, что при эффективном по Парето распределении предельная норма замещения одинакова для всех потребителей. Формальное утверждение может быть получено путем рассмотрения системы с m потребителями и n товарами, а также функцией полезности каждого потребителя как где — вектор товаров для всех i . Ограничение осуществимости для . Чтобы найти оптимальное по Парето распределение, мы максимизируем лагранжиан :
zязнак равножя(Икся){\ Displaystyle Z_ {я} = е ^ {я} (х ^ {я})}Иксязнак равно(Икс1я,Икс2я,…,Икспя){\ displaystyle x ^ {i} = (x_ {1} ^ {i}, x_ {2} ^ {i}, \ ldots, x_ {n} ^ {i})}∑язнак равно1мИксjязнак равнобj{\ displaystyle \ sum _ {я = 1} ^ {m} x_ {j} ^ {i} = b_ {j}}jзнак равно1,…,п{\ displaystyle j = 1, \ ldots, n}

Lя((Иксjk)k,j,(λk)k,(μj)j)знак равножя(Икся)+∑kзнак равно2мλk(zk-жk(Иксk))+∑jзнак равно1пμj(бj-∑kзнак равно1мИксjk){\ displaystyle L_ {i} ((x_ {j} ^ {k}) _ {k, j}, (\ lambda _ {k}) _ {k}, (\ mu _ {j}) _ {j} ) = f ^ {i} (x ^ {i}) + \ sum _ {k = 2} ^ {m} \ lambda _ {k} (z_ {k} -f ^ {k} (x ^ {k} )) + \ sum _ {j = 1} ^ {n} \ mu _ {j} \ left (b_ {j} — \ sum _ {k = 1} ^ {m} x_ {j} ^ {k} \ право)}

где и — векторы множителей. Принимая частную производную функции Лагранжа по каждому благу для и и дает следующую систему условий первого порядка:
(λk)k{\ displaystyle (\ lambda _ {k}) _ {k}}(μj)j{\ Displaystyle (\ му _ {j}) _ {j}}Иксjk{\ displaystyle x_ {j} ^ {k}}jзнак равно1,…,п{\ displaystyle j = 1, \ ldots, n}kзнак равно1,…,м{\ Displaystyle к = 1, \ ldots, м}

∂Lя∂Иксjязнак равножИксjя1-μjзнак равно для jзнак равно1,…,п,{\ displaystyle {\ frac {\ partial L_ {i}} {\ partial x_ {j} ^ {i}}} = f_ {x_ {j} ^ {i}} ^ {1} — \ mu _ {j} = 0 {\ text {for}} j = 1, \ ldots, n,}

∂Lя∂Иксjkзнак равно-λkжИксjkя-μjзнак равно для kзнак равно2,…,м и jзнак равно1,…,п,{\ displaystyle {\ frac {\ partial L_ {i}} {\ partial x_ {j} ^ {k}}} = — \ lambda _ {k} f_ {x_ {j} ^ {k}} ^ {i} — \ mu _ {j} = 0 {\ text {for}} k = 2, \ ldots, m {\ text {and}} j = 1, \ ldots, n,}

где обозначает частную производную по . Теперь исправим любые и . Из приведенного выше условия первого порядка следует, что
жИксjя{\ displaystyle f_ {x_ {j} ^ {i}}}ж{\ displaystyle f}Иксjя{\ displaystyle x_ {j} ^ {i}}k≠я{\ Displaystyle к \ neq я}j,s∈{1,…,п}{\ displaystyle j, s \ in \ {1, \ ldots, n \}}

жИксjяяжИксsяязнак равноμjμsзнак равножИксjkkжИксskk.{\ displaystyle {\ frac {f_ {x_ {j} ^ {i}} ^ {i}} {f_ {x_ {s} ^ {i}} ^ {i}}} = {\ frac {\ mu _ { j}} {\ mu _ {s}}} = {\ frac {f_ {x_ {j} ^ {k}} ^ {k}} {f_ {x_ {s} ^ {k}} ^ {k}} }.}

Таким образом, при оптимальном по Парето распределении предельная норма замещения должна быть одинаковой для всех потребителей.

Вычисление

Алгоритмы вычисления границы Парето конечного набора альтернатив изучаются в информатике и энергетике. Они включают:

• «Задача максимального вектора» или запрос горизонта .
• «Алгоритм скаляризации» или метод взвешенных сумм.
• «Метод -ограничений».ϵ{\ displaystyle \ epsilon}

Отказ от рационалистической модели

В то время господствовала рационалистическая модель человека, и герой нашего разговора был ее сторонником на протяжении многих лет. Однако однажды он от нее окончательно отказался. Согласно данной модели, поведение индивида в той или иной ситуации выглядит следующим образом: обдумывание действия, анализ его целесообразности, и наконец, поступок, приближающий к цели. Концепции Парето выглядела противоположным образом: сначала, под влиянием интереса и чувств, человек выполняет действие, а затем он объясняет его целесообразность. На этом и была построена «Теория нелогичного действия».

Тем не менее Парето не стал приверженцем иррационалистических трактовок человеческих поступков. Наоборот, он попытался сделать из рационализма «ультрарационализм», который предполагает, что в дискурсе, вместе с логикой, участвуют также наблюдения и эксперименты. Они нужны для того, чтобы разоблачить иллюзии, возникающие в нашем сознании, при желании скрыть истинные мотивы поступков.