Метод факторизации ферма

Оптимизация методом перебора делителей

Предположим, что мы пытаемся разложить на множители число n = 2345678917 методом Ферма, но кроме b вычисляем также и a − b. Начиная с n{\displaystyle {\sqrt {n}}}, можно записать:

a	48 433	48 434	48 435	48 436
b2	76 572	173 439	270 308	367 179
b	276,7	416,5	519,9	605,9
a − b	48 156,3	48 017,5	47 915,1	47 830,1

Если бы теперь для разложения числа n{\displaystyle n} стали использовать метод перебора делителей, то имело бы смысл проверять делители n{\displaystyle n} только до 47 830, а не до 48 432, так как если бы существовал делитель больше, то он был бы найден методом Ферма. Итак, всего за четыре этапа методом Ферма были проверены все делители n{\displaystyle n} от 47 830 до 48 432.

Таким образом, можно комбинировать метод Ферма с методом перебора делителей. Достаточно выбрать число c>n{\displaystyle c>{\sqrt {n}}} и использовать метод Ферма для проверки делителей между c{\displaystyle c} и n{\displaystyle {\sqrt {n}}}, а оставшиеся делители можно проверить методом перебора делителей, причём проверять делители нужно только до числа c−c2−n{\displaystyle c-{\sqrt {c^{2}-n}}}.

В примере выше, когда c=48436{\displaystyle c=48436}, делители необходимо перебирать до числа 47830. Также, к примеру, можно выбрать число c=55000{\displaystyle c=55000}, дающее границу 28937.

Комбинация методов хороша, так как при достаточной разнице между делителями числа n{\displaystyle n} метод перебора делителей эффективнее метода Ферма. Это иллюстрирует следующий пример:

a	60 001	60 002
b2	1 254 441 084	1 254 561 087
b	35 418,1	35 419,8
a − b	24 582,9	24 582,2

Явления преломления и отражения

Под отражением понимают явление, при котором свет, распространяясь в прозрачном для него веществе, встречает на своем пути препятствие и резко изменяет свою траекторию. Препятствием может быть любое: жидкое или твердое тело, прозрачное и непрозрачное.

Явление отражения было известно с глубокой древности. Согласно историческим свидетельствам, законы отражения уже были сформулированы еще до нашей эры. А в первом веке нашей эры египетский философ Герон Александрийский высказал идею о траектории света, которую впоследствии использовал француз Пьер Ферма при формулировке своего принципа.

Явление преломления заключается в изломе прямой линии, по которой движется свет, при пересечении им поверхности, разделяющей два прозрачных материала. Заметим, что в случае отражения луч движется в одном прозрачном материале или, как принято говорить, в одной среде.

Первая формулировка законов преломления приписывается персидскому математику X века, некоему Ибну Сахлю, который в своих работах опирался на труды Клавдия Птолемея (I-II века н. э.). На рубеже конца XVI — начала XVII веков голландский ученый Снелл, обобщив результаты многих экспериментов со светом, сформулировал в математическом виде 2-й закон преломления, который в настоящее время носит его фамилию. Снелл свою формулировку привел в терминах расстояний, а не углов, как это принято сейчас. Современный вид закону преломления придал уже Рене Декарт.

Запрос на вертикальные фермы

Интерес к вертикальным фермам связан с вызовами, с которыми столкнулось человечество в последние десятилетия:

• беспрецедентный рост населения планеты, чьи растущие потребности сказываются на экологии. Важнейшей из них является потребность в пище — в следующие 30 лет население планеты вырастет более чем на 2 млрд человек. Это увеличит нагрузку на сельское хозяйство и агрохимический сектор;

• увеличение средней продолжительности жизни людей также стало большим вызовом. Чем дольше человек живет, тем больше у него хронических заболеваний, тем острее необходимость поддерживать себя в форме, которая диктует высокие требования к питанию.

Хотя мы редко задумываемся об этих факторах в повседневной жизни, они напрямую влияют на формирование потребительских трендов, которым мы следуем. Среди них агентство-измеритель Nielsen выделяет:

локально произведенные продукты — они реже подвергаются химической обработке, так как не транспортируются на дальние расстояния;

эко-лейблы — интенсивное использование сельскохозяйственных угодий часто приводит к злоупотреблению химическими удобрениями, в связи с чем эко-лейблы становятся почти так же значимы, как бренды производителей;

прозрачность в коммуникациях продукта — доступ к цифровым коммуникациям формирует запрос на полную информацию о процессе производства продукта и его влиянии на окружающую среду и общество;

функциональность — продукты с полезными свойствами становятся важной составляющей рациона, позволяя компенсировать нехватку полезных веществ.

Эти тренды оказывают огромное влияние на сельское хозяйство — как на технологии производства, так и на технологии маркетинга конечной продукции. Воплощением этих изменений стала индустрия вертикальных ферм, подвергающая пересмотру все этапы цепочки производства.

Фото: Pexels

Определение внутренних сил фермы способом вырезания узлов

Ферма
может быть представлена как система
тел – узлов, соединенных между
собой связями – стержнями. Поэтому для
ее расчета справедливы правила,
изложенные в разделе равновесие систем
тел. Поскольку на каждый узел действует
система сходящихся
сил, то для него могут быть составлены
только два независимых уравнения
равновесия, из которых можно найти
только две неизвестные силы. В связи с
этим расчет следует начинать
с того узла,
к которому
приложены только две
неизвестные внутренние силы.

Рассматривая
узлы в таком порядке, чтобы в каждом
последующем было не более
двух неизвестных сил, выполняем расчет
всех реакций внутренних связей. Причем,
следует учитывать, что в соответствии
с аксиомой о действии и противодействии
силы, которыми стержень действует на
взаимодействующие с ним узлы, равны по
модулю и направлены в противоположные
стороны. Для удобства
будем обозначать их
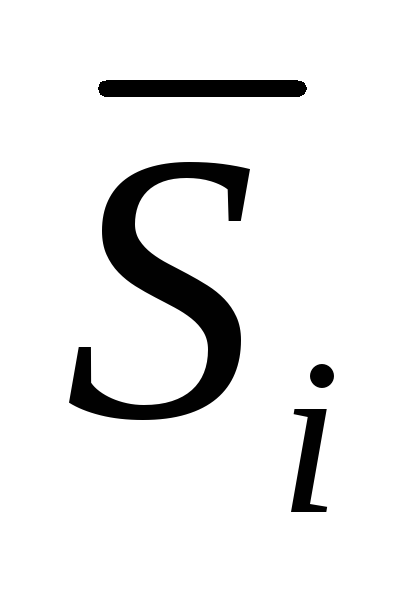и.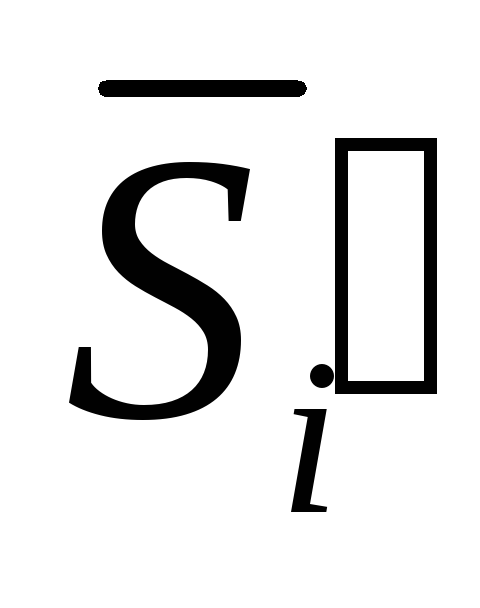

Замечание.
Для вычисления всех реакций стержней
нет необходимости рассматривать
все узлы. Последний узел может быть
использован для проверки правильности
решения.

Достоинствометода:
он легко поддается программированию
на ЭВМ.

Недостатокнакопленная
погрешность иошибка
на начальной стадии расчета ведет к
необходимости повторного
полного перерасчета.

См. также

Оценка производительности[править | править код]

Наибольшая эффективность расчета методом факторизации Ферма достигается в случае, когда множители числа n{\displaystyle n} примерно равны между собой. Это обеспечивает относительно короткий поиск последовательности

s2−n, (s+1)2−n, (s+2)2−n … (s+k)2−n.{\displaystyle s^{2}-n,\ (s+1)^{2}-n,\ (s+2)^{2}-n\ …\ (s+k)^{2}-n.}

В наихудшем варианте, когда, к примеру, a{\displaystyle a} близко к n,{\displaystyle n,} а b{\displaystyle b} близко к 1, алгоритм Ферма работает хуже по сравнению с методом перебора делителей. Число итераций для данного случая:

Iter⁡(n)=a+b2−⌈n12⌉≈n2−⌈n12⌉,{\displaystyle \operatorname {Iter} (n)={\tfrac {a+b}{2}}-\left\lceil {n}^{1/2}\right\rceil \thickapprox {\tfrac {n}{2}}-\left\lceil {n}^{1/2}\right\rceil ,} то есть, очевидно, что оно имеет порядок O(n).{\displaystyle O(n).}

Метод факторизации Ферма будет работать не хуже метода перебора делителей, если Iter⁡(n)<n12,{\displaystyle \operatorname {Iter} (n)<{n}^{1/2},} отсюда можно получить оценку для большего делителя a<4n12.{\displaystyle a<4{n}^{1/2}.} Следовательно, метод Ферма имеет экспоненциальную оценку и, как метод пробного деления, не подходит для разложения больших чисел. Можно повысить эффективность, если выполнить сначала пробное деление числа n{\displaystyle n} на числа от 2 до некоторой константы B, а затем выполнить поиск делителей методом Ферма. Такой поход помогает избавиться от малых делителей числа n{\displaystyle n}.

Описание алгоритма

Для разложения на множители нечётного числа n{\displaystyle n} ищется пара чисел (x,y){\displaystyle (x,y)} таких, что x2−y2=n{\displaystyle x^{2}-y^{2}=n}, или (x−y)⋅(x+y)=n{\displaystyle (x-y)\cdot (x+y)=n}. При этом числа (x+y){\displaystyle (x+y)} и (x−y){\displaystyle (x-y)} являются множителями n{\displaystyle n}, возможно, тривиальными (то есть одно из них равно 1, а другое — n{\displaystyle n}.)

В нетривиальном случае, равенство x2−y2=n{\displaystyle x^{2}-y^{2}=n} равносильно x2−n=y2{\displaystyle x^{2}-n=y^{2}}, то есть тому, что x2−n{\displaystyle x^{2}-n} является квадратом.

Поиск квадрата такого вида начинается с x=⌈n⌉{\displaystyle x=\left\lceil {\sqrt {n}}\right\rceil } — наименьшего числа, при котором разность x2−n{\displaystyle x^{2}-n} неотрицательна.

Для каждого значения k∈N,{\displaystyle k\in \mathbb {N} ,} начиная с k=1{\displaystyle k=1}, вычисляют (⌈n⌉+k)2−n{\displaystyle (\left\lceil {\sqrt {n}}\right\rceil +k)^{2}-n} и проверяют, не является ли это число точным квадратом. Если не является, то k{\displaystyle k} увеличивают на единицу и переходят на следующую итерацию.

Если (⌈n⌉+k)2−n{\displaystyle (\left\lceil {\sqrt {n}}\right\rceil +k)^{2}-n} является точным квадратом, то есть x2−n=(⌈n⌉+k)2−n=y2,{\displaystyle x^{2}-n=(\left\lceil {\sqrt {n}}\right\rceil +k)^{2}-n=y^{2},} то получено разложение:

n=x2−y2=(x+y)(x−y)=a⋅b,{\displaystyle n=x^{2}-y^{2}=(x+y)(x-y)=a\cdot b,} в котором x=(⌈n⌉+k){\displaystyle x=(\left\lceil {\sqrt {n}}\right\rceil +k)}

Если оно является тривиальным и единственным, то n{\displaystyle n} — простое.

На практике значение выражения на (k+1){\displaystyle (k+1)}-ом шаге вычисляется с учётом значения на k{\displaystyle k}-ом шаге:

(s+1)2−n=s2+2s+1−n,{\displaystyle \left(s+1\right)^{2}-n=s^{2}+2s+1-n,} где s=⌈n⌉+k.{\displaystyle s=\left\lceil {\sqrt {n}}\right\rceil +k.}

Формулировка принципа Ферма

Пьер Ферма был одним из известных математиков и юристов Франции в первой половине XVII века. Принцип, который носит его фамилию, он сформулировал в 1662 году, то есть спустя полвека после открытия Снеллом своего закона для преломления.

Кратко принцип Ферма может быть сформулирован так: свет при движении в абсолютно любых прозрачных средах выбирает такую траекторию, которую он пройдет за наименьшее время.

По сути, эта формулировка ничем не отличается от той, что сделал Герон Александрийский полторы тысячи лет ранее для явления отражения. Тем не менее француз сделал ее общей для всех явлений, связанных со светом, и показал, как из этого принципа могут быть получены законы преломления и отражения.

Метод Крайчика-Ферма[править | править код]

Обобщение метода Ферма было предложено в 1926 году. Он предложил рассматривать вместо пар чисел (x,y),{\displaystyle (x,y),} которые удовлетворяют соотношению x2−y2=n,{\displaystyle x^{2}-y^{2}=n,} искать пары чисел, удовлетворяющих более общему сравнению x2≡y2(modn).{\displaystyle x^{2}\equiv y^{2}{\pmod {n}}.} Такое сравнение можно найти, перемножив несколько сравнений вида ui2≡vi{\displaystyle u_{i}^{2}\equiv v_{i}}, где vi{\displaystyle v_{i}} — небольшие числа, произведения которых будет квадратом. Для этого можно рассмотреть пары чисел (ui,vi){\displaystyle (u_{i},v_{i})}, где ui{\displaystyle u_{i}} — целый числа чуть больше n{\displaystyle {\sqrt {n}}}, а vi=ui2−n{\displaystyle v_{i}=u_{i}^{2}-n}. Крайчик заметил, что многие из полученных таким образом чисел vi{\displaystyle v_{i}} раскладываются на небольшие простые множители, то есть числа vi{\displaystyle v_{i}} являются гладкими.

Последовательность действий по Крайчику

1. Найти множество пар (x,y),{\displaystyle (x,y),}которые удовлетворяют соотношению x≡y(modn).{\displaystyle x\equiv y{\pmod {n}}.}

2. Определить полное или частное разложение чисел x{\displaystyle x} и y{\displaystyle y} на множители для каждой пары (x,y).{\displaystyle (x,y).}

3. Выбрать пары (x,y),{\displaystyle (x,y),} произведение которых удовлетворит соотношению x2≡y2(modn).{\displaystyle x^{2}\equiv y^{2}{\pmod {n}}.}

4. Разложить число n{\displaystyle n} на множители.

Примерправить | править код

С помощью метода Крайчика-Ферма разложим число n=2041.{\displaystyle n=2041.} Число 46{\displaystyle 46} является первым, чей квадрат больше числа n{\displaystyle n}: 462=2116.{\displaystyle 46^{2}=2116.}

Вычислим значение функции v(u)=u2−n{\displaystyle v(u)=u^{2}-n} для всех u=46,47,…{\displaystyle u=46,47,\dots } Мы получим 75,168,263,360,459,560,…{\displaystyle 75,168,263,360,459,560,\dots }

По методу Ферма, нужно было бы продолжать вычисления пока не был бы найден квадрат какого-либо числа. По методу Крайчика-Ферма далее нужно последовательно искать такие uk{\displaystyle u_{k}}, для которых  v(u1)v(u2)…v(uk)=y2,u1u2…uk=x.{\displaystyle \ v(u_{1})v(u_{2})…v(u_{k})=y^{2},u_{1}u_{2}\dots u_{k}=x.} Тогда

x2=u12u22…uk2≡(u12−n)⋅(u22−n)⋯(uk2−n)=v(u1)⋅v(u2)⋯v(uk)=y2(modn).{\displaystyle x^{2}=u_{1}^{2}u_{2}^{2}…u_{k}^{2}\equiv (u_{1}^{2}-n)\cdot (u_{2}^{2}-n)\cdots (u_{k}^{2}-n)=v(u_{1})\cdot v(u_{2})\cdots v(u_{k})=y^{2}{\pmod {n}}.}

Из алгоритма Крайчика-Ферма следует, что все полученные числа (uk2−n){\displaystyle (u_{k}^{2}-n)} можно легко факторизовать.

Действительно: 75=3⋅52, 168=23⋅3⋅7, 360=23⋅32⋅5, 560=24⋅5⋅7.{\displaystyle 75=3\cdot 5^{2},\ 168=2^{3}\cdot 3\cdot 7,\ 360=2^{3}\cdot 3^{2}\cdot 5,\ 560=2^{4}\cdot 5\cdot 7.}

Очевидно, что произведение полученных четырёх чисел будет квадратом: 210⋅34⋅54⋅72.{\displaystyle 2^{10}\cdot 3^{4}\cdot 5^{4}\cdot 7^{2}.} Тогда теперь можно вычислить x,y{\displaystyle x,y:}

x=46⋅47⋅49⋅51≡311(mod2041), y=25⋅32⋅52⋅7≡1416(mod2041).{\displaystyle x=46\cdot 47\cdot 49\cdot 51\equiv 311{\pmod {2041}},\ y=2^{5}\cdot 3^{2}\cdot 5^{2}\cdot 7\equiv 1416{\pmod {2041}}.}

Далее с помощью алгоритма Евклида находим gcd(1416−311,2041)=13{\displaystyle \gcd(1416-311,2041)=13}.

Таким образом, 2041=13⋅157.{\displaystyle 2041=13\cdot 157.}

Описание алгоритма

Для разложения на множители нечётного числа n{\displaystyle n} ищется пара чисел (x,y){\displaystyle (x,y)} таких, что x2−y2=n{\displaystyle x^{2}-y^{2}=n}, или (x−y)⋅(x+y)=n{\displaystyle (x-y)\cdot (x+y)=n}. При этом числа (x+y){\displaystyle (x+y)} и (x−y){\displaystyle (x-y)} являются множителями n{\displaystyle n}, возможно, тривиальными (то есть одно из них равно 1, а другое — n{\displaystyle n}.)

В нетривиальном случае, равенство x2−y2=n{\displaystyle x^{2}-y^{2}=n} равносильно x2−n=y2{\displaystyle x^{2}-n=y^{2}}, то есть тому, что x2−n{\displaystyle x^{2}-n} является квадратом.

Поиск квадрата такого вида начинается с x=⌈n⌉{\displaystyle x=\left\lceil {\sqrt {n}}\right\rceil } — наименьшего числа, при котором разность x2−n{\displaystyle x^{2}-n} неотрицательна.

Для каждого значения k∈N,{\displaystyle k\in \mathbb {N} ,} начиная с k=1{\displaystyle k=1}, вычисляют (⌈n⌉+k)2−n{\displaystyle (\left\lceil {\sqrt {n}}\right\rceil +k)^{2}-n} и проверяют, не является ли это число точным квадратом. Если не является, то k{\displaystyle k} увеличивают на единицу и переходят на следующую итерацию.

Если (⌈n⌉+k)2−n{\displaystyle (\left\lceil {\sqrt {n}}\right\rceil +k)^{2}-n} является точным квадратом, то есть x2−n=(⌈n⌉+k)2−n=y2,{\displaystyle x^{2}-n=(\left\lceil {\sqrt {n}}\right\rceil +k)^{2}-n=y^{2},} то получено разложение:

n=x2−y2=(x+y)(x−y)=a⋅b,{\displaystyle n=x^{2}-y^{2}=(x+y)(x-y)=a\cdot b,} в котором x=(⌈n⌉+k){\displaystyle x=(\left\lceil {\sqrt {n}}\right\rceil +k)}

Если оно является тривиальным и единственным, то n{\displaystyle n} — простое.

На практике значение выражения на (k+1){\displaystyle (k+1)}-ом шаге вычисляется с учётом значения на k{\displaystyle k}-ом шаге:

(s+1)2−n=s2+2s+1−n,{\displaystyle \left(s+1\right)^{2}-n=s^{2}+2s+1-n,} где s=⌈n⌉+k.{\displaystyle s=\left\lceil {\sqrt {n}}\right\rceil +k.}

Где инопланетяне?

Популярная гипотеза относительно галактической колонизации заключается в том, что ее можно достичь с помощью космического корабля, который может путешествовать на близлежащие планеты, провести там пару столетий, при этом самореплицируясь, а затем отправить эти реплики в другие миры.

Поиск планет Земля | Изображение предоставлено: НАСА

При этом, даже не приблизившись к скорости света, цивилизация сможет колонизировать всю галактику менее чем за 4 миллиона лет, относительно короткое время в космическом масштабе.

Если мы предположим, что только один процент разумной жизни выживет достаточно долго, чтобы стать цивилизацией, колонизирующей галактику, их присутствие все равно будет довольно заметно. И все же мы ничего не видим, ничего не слышим, и нас никто не посещает.

Таков, по крайней мере, в сущности, парадокс Ферми. Если жизнь существует на других планетах, почему мы никогда ни от кого ничего не слышали? Чтобы понять этот парадокс, мы сначала должны узнать о чем-то, что называется шкалой Кардашева. Она объединяет разумные цивилизации в три различные категории.

Цивилизация типа I: Цивилизация типа I обладает способностью использовать всю энергию, доступную на их планете. В масштабе от 0 до 1, одна из которых является цивилизацией типа I, Земля Земля в настоящее время составляет 0,7. Мы должны быть в состоянии достичь этого уровня в следующем столетии или около того.

Цивилизация типа II: Цивилизация типа II должна использовать всю энергию своей домашней звезды.

Цивилизация типа III: Третий и последний тип цивилизации в Шкале Кардашева контролирует все в своей галактике.

Если есть какая-либо цивилизация старше нашей, которая способна выжить вплоть до типа III, то более или менее вероятно, что они освоили межгалактическое путешествие и, возможно, колонизируют другие планеты.

Существующие данные

Наша Солнечная система, если наблюдать её с расстояния в несколько десятков световых лет, была бы очень необычной в связи с огромным уровнем радиоизлучения (созданного радиостанциями) у ничем не приметной звезды. Можно допустить, что подобное излучение у соседней звезды было бы также сразу определено как необычное земными астрономами. С другой стороны, чем дальше удалена звезда, тем более устаревшие данные о ней мы имеем. Так, например, на расстоянии в 150 световых лет радиопередачи Земли будут принципиально необнаружимы до 2045 года, так как беспроводная связь известна на Земле с 1895 года, и как следствие, первые радиопередачи ещё не прошли такое расстояние.

Данные радио- и визуальных наблюдений накапливались на протяжении нескольких десятилетий в рамках проектов «Озма», SETI и других инициатив, имевших целью поиск обитаемых планет за пределами Солнечной системы. До сих пор не обнаружено ни одной звезды солнечного типа, которая бы демонстрировала необычно интенсивное радиоизлучение — из чего, похоже, можно сделать вывод, что мы являемся единственным видом, использующим радиоволны в нашей части Галактики. К тому же большинство планет, выявленных за пределами Солнечной системы, вероятно, характеризуются слишком суровыми условиями для эволюции развитых форм жизни.

Сторонники теории о наличии внеземной жизни приводят следующие объяснения этим фактам:

• Другие разумные виды могут использовать направленные приборы связи — например, лазеры. Возможно, они используют для связи нейтрино или другие, пока неизвестные нам частицы.
• Найти планеты с нестабильными орбитами легче. Из-за этого у наблюдателя создаётся впечатление о том, что большинство планет обладают именно нестабильными орбитами, при которых жизнь невозможна. Вследствие этого недооценивается количество пригодных для жизни планет.
• Другие разумные виды слишком далеко ушли от нас в развитии. Предполагается, что многие ранее появившиеся цивилизации могли уже стать настолько могущественными, что мы неспособны отличить их деятельность от природных явлений, вопреки гипотезе «космических чудес», которые в 1960-х предлагал искать Иосиф Шкловский.
• Ещё одним интересным фактом является то, что в связи с развитием оптоволоконных систем связи, отказом от мощных радиостанций и переходом на маломощные сотовые системы связи, кабельное и спутниковое телевидение и радиовещание радиоизлучение Земли в последние годы начало уменьшаться. Таким образом, активный период «свечения» Земли в радиодиапазоне составил немногим более 100 лет, что является крайне малым сроком в сравнении с продолжительностью существования цивилизации и даёт дополнительный аргумент сторонникам существования внеземной разумной жизни.
• Существует , согласно которой разумные и развитые цивилизации не могут вступить в космическую эру из-за очень значительной силы притяжения, вследствие которой использование химических двигателей становится практически бесполезным.
• Китайский писатель-фантаст Лю Цысинь предложил для объяснения парадокса Ферми концепцию «тёмного леса». Суть концепции в том, что эволюция жизни во Вселенной подразумевает войну на выживание среди достаточно развитых цивилизаций, потому всякая достаточно развитая цивилизация тщательно скрывает следы своего присутствия во Вселенной, чтобы не подвергнуться удару со стороны цивилизаций-конкурентов. Те же молодые цивилизации, которые выдают своё существование, подобны человеку, идущему через тёмный лес: ему кажется, будто он здесь один, но как-только он крикнет «Ау!» достаточно громко, какая-нибудь тварь из темноты набросится на него, и такой человек даже не поймёт, кто и каким образом его убил.

Вывод закона преломления Снелла

Теперь покажем, как можно вывести из принципа Ферма закон преломления света. Для этого рассмотрим рисунок, похожий на предыдущий.

Для простоты будем рассматривать случай в плоскости xy. Выпишем координаты источника S и приемника P света, которые находятся в разных средах:

Найдем неизвестную координату точки M. Координата y=0 для нее точно известна, поскольку именно на границе сред (ось x) меняется скорость распространения света. Длины отрезков SM и MP равны:

Общее время, которое затратит свет на прохождение траектории SMP, будет равно:

Здесь v₁, v₂ — скорости луча в соответствующих средах. Чтобы найти минимальное время движения, следует взять полную производную по переменной x и приравнять ее к нулю. Получаем:

Используя функции синусов угла падения θ₁ и преломления θ₃, получаем:

Чтобы привести полученное равенство к закону Снелла в удобном виде (через показатели преломления сред), необходимо помножить левую и правую части на скорость света c.

Таким образом, применение принципа Ферма позволяет легко вывести законы для основных явлений движения светового луча в прозрачных материалах.

Вывод 1-го закона отражения

Пользуясь принципом Ферма, законы отражения получим математически. Для этого рассмотрим рисунок ниже.

Здесь показано, что луч выходит с точки S, которая лежит на оси y. Затем он отражается от плоскости xz в некоторой неизвестной точке M. После отражения луч движется к точке P, лежащей на плоскости xy. Выбранное положение точек S и P не влияет на общность дальнейших рассуждений, а лишь упрощает математические выкладки.

Итак, запишем координаты каждой точки:

Координаты положения точек S и P известны. Задача состоит в том, чтобы найти такую точку M, которая будет соответствовать реальной траектории SMP, пройденной световым лучом. Также будем полагать, что рассматриваемое пространство является однородным, то есть скорость света в любой точке является постоянной величиной.

Согласно принципу Ферма, траекторию SMP свет пройдет за наименьшее время, если она будет наиболее короткой из всех возможных. Запишем ее длину:

Чтобы вычислить минимальную длину SMP, необходимо найти частные производные по x и z (неизвестные координаты точки M) и приравнять к нулю полученные результаты.

Сначала найдем частную производную по z. Имеем:

Это равенство имеет единственный корень, когда z = 0. Иными словами, точка M лежит на оси x, то есть в той же плоскости, что и точки P и S (плоскость xy). Откуда следует, что восстановленная нормаль к плоскости xz, в которой, по условию задачи, находится точка M, будет лежать вместе с SM и MP в одной плоскости (xy). Это и есть 1-й закон отражения.

Вывод распределения

Распределение Ферми — Дирака как функция от ε. Высокоэнергетические состояния имеют меньшую вероятность. Или, низкоэнергитические состояния более вероятны

где

— энергия состояния s,

— число частиц, находящихся в состоянии s,

— химический потенциал,

s — это индекс, пробегающий все возмножные микросостояния системы.

В данном контексте, система имеет фиксированные состояния. Итак, если какое либо состояние занято n частицами, то энергия системы — . Если состояние свободно, то энергия имеет значение . Будем рассматривать равновесные одночастичные состояния как резервуар. После того, как система и резервуар займут одно и тоже физическое пространство, начинает происходить обмен частицами между двумя состояниями (фактически, это явление мы и исследуем). Отсюда становится ясно, почему используется описанная выше функция распределения, которая, через химический потенциал, учитывает поток частиц между системой и резервуаром.

Для фермионов, каждое состояние может быть либо занято одной частицей, либо свободно. Поэтому, наша система имеет два множества: занятых (разумеется, одной частицей) и незанятых состояний, обозначающихся and соответственно. Видно, что , , и , . Поэтому функция распределения принимает вид:

.

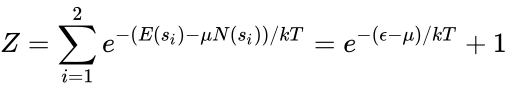Для большого канонического ансамбля, вероятность того, что система находится в микросостоянии вычисляется по формуле

.

Наличие состояния, занятого частицей, означает, что система находится в микросостоянии , вероятность которого

.

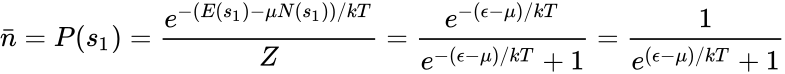называется распределением Ферми — Дирака. Для фиксированной температуры T, есть вероятность того, что состояние с энергией ε будет занято фермионом

Обратите внимание, что
является убывающей функцией от ε. Это соответствует нашим ожиданиям: высокоэнергетические состояния занимаются с меньшей вероятностью.

Обратите внимание, что энергетический уровень ε имеет вырождение. Теперь можно произвести простую модификацию:

.

Это число — ожидаемое число частиц, в суммарном состоянии с энергией ε.

Для всех температур T, . Это означает, что состояния с энергией μ всегда будут иметь одинаковую вероятность быть заполнеными или свободными.

В пределе , становится ступенчатой функцией (см. первый график). Все состояния с энергией меньше химического потенциала μ будут заняты с вероятностью 1. Состояния с энергией выше химического потенциала μ будут свободны. Химический потенциал при нулевой температуре — энергия Ферми, обозначается , то есть

.