Что такое число

Натуральные числа

НАТУРАЛЬНЫЕ ЧИСЛА — это числа, которые используются при счёте. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …, 1 — самое маленькое число, а самого большого числа не существует. Число 0 (нуль) обозначает отсутствие предмета.  Нуль НЕ является натуральным числом.

Разряды и классы  натуральных чисел

Для записи чисел используется ДЕСЯТИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ. В десятичной системе счисления пользуются единицами, десятками единиц, десятками десятков — сотнями и т. д. Каждая новая единица счёта больше предыдущей ровно в 10 раз:

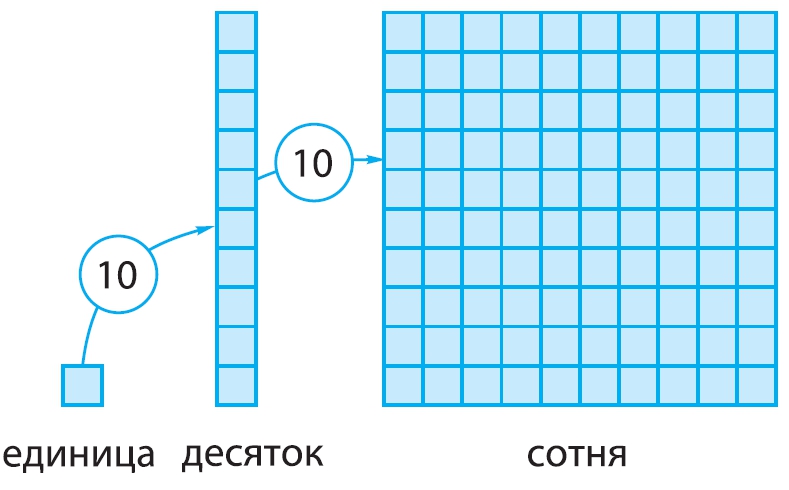
Десятичная система счисления — позиционная. В этой системе счисления значение каждой цифры в записи числа зависит от её позиции (места).

Позиция (место) цифры в записи числа называется РАЗРЯДОМ. Самый младший разряд — ЕДИНИЦЫ. Затем следуют ДЕСЯТКИ, СОТНИ, ТЫСЯЧИ и т. д.

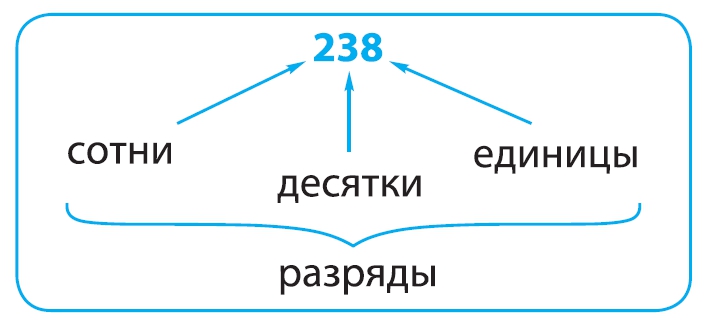
Каждые три разряда натуральных чисел образуют КЛАСС.

Плакат «Сделай уроки сам!» 3-4 класс  https://делайурокисам.рф

Основной вопрос, который родители часто задают: зачем ребенку эти знания? Ответ на этот вопрос очень простой — после изучения этого материала, дети переходят к таким темам как сложение и вычитание в столбик, где обязательно необходимо знать разряды числа, чтобы правильно вычислить примеры.

И если ребенок не освоит эту тему, тогда он не сможет правильно решать в столбик.

Сложение столбиком

    А) Складываем единицы: 4 + 3 = 7.           Записываем под единицами.      Б) Складываем десятки: 4 + 3 = 7.            Записываем под десятками.      В) Складываем сотни: 4 + 3 = 7.            Записываем под сотнями.                                                  Ответ: 777

Вычитание столбиком

        А) Вычитаем единицы: 9 – 3 = 6.               Записываем под единицами.         Б) Вычитаем десятки: 0 меньше,              чем 2, занимаем в сотнях (тысячах).

            10 – 2 = 8. Записываем под десятками.                                            В) Вычитаем сотни: 9 – 4 = 5.                                                 Записываем под сотнями.                                                 Ответ: 586

Справочная информация

ДокументыЗаконыИзвещенияУтверждения документовДоговораЗапросы предложенийТехнические заданияПланы развитияДокументоведениеАналитикаМероприятияКонкурсыИтогиАдминистрации городовПриказыКонтрактыВыполнение работПротоколы рассмотрения заявокАукционыПроектыПротоколыБюджетные организацииМуниципалитетыРайоныОбразованияПрограммыОтчетыпо упоминаниямДокументная базаЦенные бумагиПоложенияФинансовые документыПостановленияРубрикатор по темамФинансыгорода Российской Федерациирегионыпо точным датамРегламентыТерминыНаучная терминологияФинансоваяЭкономическаяВремяДаты2015 год2016 годДокументы в финансовой сферев инвестиционной

Появление чисел

Интуитивное представление о числе, по–видимому, так же старо, как и само человечество, хотя с достоверностью проследить все ранние этапы его развития в принципе невозможно. Прежде чем человек научился считать или придумал слова для обозначения чисел, он, несомненно, владел наглядным, интуитивным представлением о числе, позволявшим ему различать одного человека и двух людей или двух и многих людей. То, что первобытные люди сначала знали только “один”, “два” и “много”, подтверждается тем, что в некоторых языках, например в греческом, существуют три грамматические формы: единственного числа, двойственного числа и множественного числа. Позднее человек научился делать различия между двумя и тремя деревьями и между тремя и четырьмя людьми. Счет изначально был связан с вполне конкретным набором объектов, и самые первые названия чисел были прилагательными. Например, слово “три” использовалось только в сочетаниях “три дерева” или “три человека”; представление о том, что эти множества имеют между собой нечто общее – понятие троичности – требует высокой степени абстракции. О том, что счет возник раньше появления этого уровня абстракции, свидетельствует тот факт, что слова “один” и “первый”, равно как “два” и “второй”, во многих языках не имеют между собой ничего общего, в то время как лежащие за пределами первобытного счета “один”, “два”, “много”, слова “три” и “третий”, “четыре” и “четвертый” ясно указывают на взаимосвязь между количественными и порядковыми числительными.

Названия чисел, выражающие весьма абстрактные идеи, появились, несомненно, позже, чем первые грубые символы для обозначения числа объектов в некоторой совокупности. В глубокой древности примитивные числовые записи делались в виде зарубок на палке, узлов на веревке, выложенных в ряд камешков, причем подразумевалось, что между пересчитываемыми элементами множества и символами числовой записи существует взаимно однозначное соответствие. Но для чтения таких числовых записей названия чисел непосредственно не использовались. Ныне мы с первого взгляда распознаем совокупности из двух, трех и четырех элементов; несколько труднее распознаются на взгляд наборы, состоящие из пяти, шести или семи элементов. А за этой границей установить на глаз их число практически уже невозможно, и нужен анализ либо в форме счета, либо в определенном структурировании элементов. Счет на бирках, по–видимому, был первым приемом, который использовался в подобных случаях: зарубки на бирках располагались определенными группами подобно тому, как при подсчете избирательных бюллетеней их часто группируют пачками по пять или десять штук. Очень широко был распространен счет на пальцах, и вполне возможно, что названия некоторых чисел берут свое начало именно от этого способа подсчета.

Важная особенность счета заключается в связи названий чисел с определенной схемой счета. Например, слово “двадцать три” – не просто термин, означающий вполне определенную (по числу элементов) группу объектов; это термин составной, означающий “два раза по десять и три”. Здесь отчетливо видна роль числа десять как коллективной единицы или основания; и действительно, многие считают десятками, потому что, как отметил еще Аристотель, у нас по десять пальцев на руках и на ногах. По той же причине использовались основания пять или двадцать. На очень ранних стадиях развития истории человечества за основания системы счисления принимались числа 2, 3 или 4; иногда для некоторых измерений или вычислений использовались основания 12 и 60.

Считать человек начал задолго до того, как он научился писать, поэтому не сохранилось никаких письменных документов, свидетельствовавших о тех словах, которыми в древности обозначали числа. Для кочевых племен характерны устные названия чисел, что же касается письменных, то необходимость в них появилась лишь с переходом к оседлому образу жизни, образованием земледельческих сообществ. Возникла и необходимость в системе записи чисел, и именно тогда было заложено основание для развития математики.

Примечания

1. ↑
2. .
3. Нуль // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3. — С. 1082.
4. Нуль // Большой Энциклопедический словарь (рус.). — 2000. // Большой Энциклопедический словарь. 2000.
5. Большой толковый словарь русского языка. Гл. ред. С. А. Кузнецов. Первое издание: СПб.: Норинт, 1998.
6. ↑ Потапов М. К., Александров В. В., Пасиченко П. И. Алгебра и анализ элементарных функций. — М.: Наука, 1981. — С. 9. — 560 с.
7. . NCSU COE People. Дата обращения 12 августа 2019.
8. ↑ Савин А. П. Энциклопедический словарь юного математика / сост. А. П. Савин. — М.: «Педагогика», 1989. — С. 219.
9. Брич З. С., Воюш В. И., Дегтярёва Г. С., Ковалевич Э. В. Программирование на языке Ассемблера ЕС ЭВМ. — М.: Статистика, 1976. — 296 с. — С. 13—14, 19.
10. Кулаковская В. П., Романовская Л. М., Савченко Т. А., Фельдман Л. С. Кобол ЭВМ Минск-32. Пособие для работников вычислительных центров. — М.: Статистика, 1973. — 284 с.
11. Брябрин В. М. Программное обеспечение персональных ЭВМ. 3-е изд. — М.: Наука, 1990. — 272 с. — ISBN 5-02-014824-5. — С. 17, 113—114.
12. Смирнов Н. Н. Программные средства персональных ЭВМ. — Л.: Машиностроение, 1990. — 272 с. — ISBN 5-217-00029-5. — С. 13, 80—81.
13. Ламберто Гарсия дель Сид. Особые числа других культур → 116 // Замечательные числа. Ноль, 666 и другие бестии. — DeAgostini, 2014. — Т. 21. — С. 116. — 159 с. — (Мир математики). — ISBN 978-5-9774-0716-8.
14. .
15.  (англ.). The Guardian (14 September 2017). Дата обращения 19 сентября 2017.
16. Ламберто Гарсия дель Сид. Особые числа других культур → 116 // Замечательные числа. Ноль, 666 и другие бестии. — DeAgostini, 2014. — Т. 21. — С. 115. — 159 с. — (Мир математики). — ISBN 978-5-9774-0716-8.
17. «Zentralblatt für Mathematik», апрель, 1957, сообщение чешского историка математики Г. Феттера.
18. Депман И. Я. История Арифметики. — изд. «Просвещение», Москва, 1965, стр. 89.
19. Депман И. Я. История Арифметики. — изд. «Просвещение», Москва, 1965, стр.90
20. Joseph, George Gheverghese. The Crest of the Peacock: Non-European Roots of Mathematics (Third Edition) (англ.). — Princeton University Press, 2011. — P. 86. — ISBN 978-0-691-13526-7.

Число в философии

Философское понимание числа заложили пифагорейцы. Аристотель свидетельствует, что пифагорейцы считали числа «причиной и началом» вещей, а отношения чисел — основой всех отношений в мире. Числа придают миру упорядоченность и делают его космосом. Такое отношение к числу было принято Платоном, а позже неоплатониками. Платон при помощи чисел различает подлинное бытие (то, что существует и мыслится само по себе), и неподлинное бытие, (то, что существует лишь благодаря другому и познаётся только в отношении). Срединное положение между ними занимает число. Оно придаёт меру и определённость вещам и делает их причастными бытию. Благодаря числу вещи могут быть подвергнуты пересчёту и поэтому они могут быть мыслимы, а не только ощущаемы. Неоплатоники, особенно Ямвлих и Прокл, почитали числа столь высоко, что даже не считали их сущими — устроение мира исходит от числа, хотя и не непосредственно. Числа сверхсущны, пребывают выше Ума, и недоступны знанию. Неоплатоники различают божественные числа (прямую эманацию Единого) и математические числа (составленные из единиц). Последние являются несовершенными подобиями первых. Аристотель, наоборот, приводит целый ряд аргументов, показывающих, что утверждение о самостоятельном существовании чисел приводит к нелепостям. Арифметика выделяет в этих реально сущих вещах только один аспект и рассматривает их с точки зрения их количества. Числа и их свойства являются результатом такого рассмотрения. Кант считал, что явление познано тогда, когда оно сконструировано в соответствии с априорными понятиями — формальными условиями опыта. Число — одно из таких условий. Число задаёт конкретный принцип или схему конструирования. Любой объект является исчислимым и измеряемым, потому что он сконструирован по схеме числа (или величины). Поэтому всякое явление может рассматриваться математикой. Разум воспринимает природу подчинённой числовым закономерностям именно потому, что сам строит её в соответствии с числовыми закономерностями. Так объясняется возможность применения математики в изучении природы. Математические определения, разработанные в XIX веке, были серьёзно пересмотрены в начале XX века. Это было вызвано не столько математическими, сколько философскими проблемами. Определения, которые были даны Пеано, Дедекиндом или Кантором, и которые используются в математике и в настоящее время, нужно было обосновать с помощью фундаментальных принципов, коренящихся в самой природе знания. Различают три таких философско-математических подхода: логицизм, интуиционизм и формализм. Философскую базу логицизма разработал Рассел. Он полагал, что истинность математических аксиом неочевидна. Истинность обнаруживается сведением к наиболее простым фактам. Отражением таких фактов Рассел считал аксиомы логики, которые он положил в основу определения числа. Важнейшим понятием у него является понятие класса. Натуральное число η есть класс всех классов, содержащих η элементов. Дробь — это уже не класс, а отношение классов. Интуицист Брауэр имел противоположную точку зрения: логику он считал лишь абстракцией от математики, рассматривал натуральный ряд чисел как базовую интуицию, лежащую в основании всякой мыслительной деятельности. Гильберт, главный представитель формальной школы, видел обоснование математики в построении непротиворечивой аксиоматической базы, в пределах которой можно бы было формально обосновать любое математическое понятие. В разработанной им аксиоматической теории действительных чисел представление о числе лишается всякой глубины и сводится лишь к графическому символу, подставляемому по определённым правилам в формулы теории.

Представление чисел в памяти компьютера

подробнее см. Прямой код, Дополнительный код (представление числа), Число с плавающей запятой

Для представления натурального числа в памяти компьютера, оно обычно переводится в двоичную систему счисления. Для представления отрицательных чисел часто используется дополнительный код числа, который получается путём прибавления единицы к инвертированному представлению модуля данного отрицательного числа в двоичной системе счисления.

Представление чисел в памяти компьютера имеет ограничения, связанные с ограниченностью объёма памяти, выделяемого под числа. Даже натуральные числа представляют собой математическую идеализацию, ряд натуральных чисел бесконечен. На объём же памяти ЭВМ накладываются физические ограничения. В связи с этим в ЭВМ мы имеем дело не с числами в математическом смысле, а с некоторыми их представлениями, или приближениями. Для представления чисел отводится некоторое определенное число ячеек (обычно двоичных, бит — от BInary digiT) памяти. В случае, если в результате выполнения операции полученное число должно занять больше разрядов, чем отводится в ЭВМ, результат вычислений становится неверным — происходит так называемое арифметическое переполнение. Действительные числа обычно представляются в виде чисел с плавающей запятой. При этом лишь некоторые из действительных чисел могут быть представлены в памяти компьютера точным значением, в то время как остальные числа представляются приближёнными значениями. В наиболее распространённом формате число с плавающей запятой представляется в виде последовательности битов, часть из которых кодирует собой мантиссу числа, другая часть — показатель степени, и ещё один бит используется для указания знака числа.

Иерархия чисел

Ниже представлена иерархия чисел, для множеств которых справедливо выражение N⊂Z⊂Q⊂R⊂C⊂H⊂O⊂S{\displaystyle \mathbb {N} \subset \mathbb {Z} \subset \mathbb {Q} \subset \mathbb {R} \subset \mathbb {C} \subset \mathbb {H} \subset \mathbb {O} \subset \mathbb {S} }, с примерами:

Обобщения чисел

Кватернионы представляющие собой разновидность гиперкомплексных чисел. Множество кватернионов обозначается H{\displaystyle \mathbb {H} }. Кватернионы в отличие от комплексных чисел не коммутативны относительно умножения.

В свою очередь октавы O{\displaystyle \mathbb {O} }, являющиеся расширением кватернионов, уже теряют свойство ассоциативности.

В отличие от октав, седенионы S{\displaystyle \mathbb {S} } не обладают свойством альтернативности, но сохраняют свойство степенной ассоциативности.

Для этих множеств обобщённых чисел справедливо следующее выражение: C⊂H⊂O⊂S{\displaystyle \mathbb {C} \subset \mathbb {H} \subset \mathbb {O} \subset \mathbb {S} }

p-адические числа Qp{\displaystyle \mathbb {Q} _{p}} можно рассматривать как элементы поля, являющегося пополнением поля рациональных чисел Q{\displaystyle \mathbb {Q} } при помощи т. н. , аналогично тому, как поле действительных чисел R{\displaystyle \mathbb {R} } определяется как его пополнение при помощи обычной абсолютной величины.

Аде́ли определяются как бесконечные последовательности {a_∞,a₂,a₃,…a_p…}, где a_∞ — любое действительное число, а a_p — p-адическое, причём все a_p, кроме, может быть, конечного их числа, являются целыми p-адическими. Складываются и умножаются адели покомпонентно и образуют кольцо. Поле рациональных чисел вкладывается в это кольцо обычным образом r→{r, r,…r,…}. Обратимые элементы этого кольца образуют группу и называются иде́лями.

Практически важным обобщением числовой системы является интервальная арифметика.

Арифметические действия с числами

Основными арифметическими действиями в математике являются:

• сложение,
• вычитание,
• умножение,
• деление.

Каждый результат этих действий также имеет своё название:

• сумма — результат, получившийся при сложении чисел,
• разность — результат, получившийся при вычитании чисел,
• произведение — результат умножения чисел,
• частное — результат деления.

Более простым языком объясняя понятия суммы, разности, произведения и частного в математике, можно упрощённо записать их лишь как словосочетания:

• сумма — прибавить,
• разность — отнять,
• произведение — умножить,
• частное — разделить.

Разность в математике

Рассматривая определения, что же такое разность чисел в математике, можно обозначить это понятие несколькими способами:

• Разность чисел означает, насколько одно из них больше другого.
• Разностью в математике называется итог, получившийся при отнимании друг от друга двух и более чисел.
• Это вычитание одного числа из другого.
• Это цифра, составляющая остаток при минусовании двух величин.
• Это величина, являющаяся результатом вычитания двух значений.
• Разность показывает количественное различие между двумя цифрами.
• Это результат одного из четырёх арифметических действий, которым является вычитание.
• Это то, что получится, если из уменьшаемого отнять вычитаемое.

И все эти определения являются верными.

Как найти разницу величин

Возьмём за основу то обозначение разности, которое нам предлагает школьная программа:

Разностью называется результат вычитания одного числа из другого. Первое из этих чисел, из которого осуществляется вычитание, называется уменьшаемым, а второе, которое вычитают из первого, называется вычитаемым.

Ещё раз прибегнув к школьной программе, мы находим правило, как найти разность:

Чтобы найти разность, надо от уменьшаемого отнять вычитаемое.

Всё понятно. Но при этом мы получили ещё несколько математических терминов. Что они значат?

• Уменьшаемое — это математическое число, от которого отнимают и оно уменьшается (становится меньше).
• Вычитаемое — это математическое число, которое вычитают из уменьшаемого.

Теперь понятно, что разность состоит из двух чисел, которые для её вычисления должны быть известны. А как их найти тоже воспользуемся определениями:

• Чтобы найти уменьшаемое, надо к вычитаемому прибавить разность.
• Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.

Системы счисления

Система счисления – это некий вариант представления чисел.

К примеру, представьте, что перед вами лежит несколько яблок. Вы хотели бы узнать, сколько яблок лежат на столе? Для этого вы могли бы считать, загибая пальцы рук или делать зарубки на дереве. А могли бы вы и представить, что десять яблок – это одна корзинка, а одно яблоко – это одна спичка. Спички по ходу счета выкладывать на столе под одной.

В первом варианте подсчета число получилось в виде строки из зарубок на дереве (или загнутых пальцев рук), а во втором варианте подсчета – это был набор из корзинок и спичек. Слева должны быть емкости, а справа — спички.

Системы счисления бывают двух видов:

1. Позиционные.
2. Непозиционные.

Позиционные системы счисления бывают:

• Однородными.
• Смешанными.

Непозиционной называют такую систему счисления, в которой цифра в числе соотносится с такой величиной, которая не зависит от ее разряда. Поэтому, если у вас пять зарубок, то число будет равно пяти. Ибо каждой зарубке будет соответствовать одно яблоко.

Позиционной системой счисления является та, в которой цифра в числе будет зависеть от ее разряда.

Та система счисления, к которой мы привыкли – это десятичная система счета. Она позиционная.

Когда наши предки начали учиться считать, у них появилась идея записывать числа. изначально они использовали те самые зарубки на деревьях или камнях, где каждая черточка обозначала какой-либо предмет (одно яблоко, к примеру). Именно так и была изобретена единичная система счисления.

Цифра и число

Число — это понятие, которое обозначает количество.

Цифра — это символ или знак, который обозначает число.

Количество цифр в числе может быть разным, от одного до бесконечности.

К примеру, дано число «семь», которое отражает количество чего-либо. Но это самое число мы записываем цифрой 7.

Определение цифры и числа на простом языке приведем ниже.

Числа необходимы для того, чтобы вести счет каких-либо предметов, замерять длину, измерять время, скорость и другие величины. А цифра — это такой символ, который показывает число визуально, понятно и наглядно.

Грубо говоря, цифру можно сравнить с буквой из алфавита, а слово — с числом. То есть существует всего 33 знака (символа) в русском языке для обозначения букв. С их помощью можно записать сколько угодно слов. И существует всего десять цифр для обозначения чисел.

Давайте наглядно разберем, чем отличается цифра от числа.

Для того чтобы написать число 587, мы будем использовать три цифры: 5, 8 и 7. Сами по себе цифры никак не могут отразить целое число. Этими же цифрами мы можем записать еще много разных чисел. К примеру 857, 875 878755 и так далее.

Навигация

Внесистемные числа

Кроме чисел, которые записаны при помощи английской или американской систем, известны внесистемные числа. У них есть собственные названия, в которых нет латинских префиксов. Для понимания сначала рассмотрим запись латинскими числительными.

Единица – это 100, десять — 101 и так далее: миллиард — 109, триллион — 1012, квадриллион — 1015, квинтиллион — 1018, секстиллион — 1021, септиллион — 1024, октиллион — 1027, нониллион — 1030, дециллион — 1033.

С помощью приставок можно и дальше выводить числа: андециллион, дуодециллион, тридециллион и так далее. Но нужны собственные названия чисел, а тут только составные названия. Поэтому по этой системе собственных имен еще только три — вигинтиллион — 1063, центиллион — 10303, миллеиллион — 103003.

В миллеиллионе 3003 нуля

Число с собственным, а не составным названием больше 103003 получить невозможно. Однако числа больше миллеиллиона известны – это внесистемные числа.

Самое маленькое внесистемное число носит название мириада. Означает сотню сотен, т.е. 10000.

Далее идет гугол. Это десять в сотой степени — 1010100. Единица со ста нулями. О гуголе впервые написали в 1938 году. Американский математик Эдвард Каснер сказал, что назвать большое число таким образом предложил племянник. А популярным это название стало после того, как в честь него назвали поисковик «Google».

Число гугол

Далее встречается число асанкхейя. Это 1010140. Следом идет число гуголплекс. Его придумал тот же Каснер с племянником. Означает 10 в степени 10 в степени 100. Или единица с гуголом нулей.

Еще больше гуголплекса число Скьюза. Его предложил Скьюз в 1933 году во время доказательства гипотезы Риманна о простых числах.

Обозначается — Sk1.

Есть второе число Скьюза. Обозначается как Sk2. Вводится, если гипотеза Риманна не справедлива. Второе число Скьюза равно

Но и это число не предел. Самое большое число, которое применяется в математическом доказательстве, это число Грэма. Его использовали впервые в 1977 году в доказательстве оценки в теории Рамсея.

Число выражено в 64-уровневой схеме, вывел которую Кнут в 1978 году. Ученый придумал понятие сверхстепень и предложил записывать ее стрелками вверх. В итоге число Грэма G63, или просто G, — самое большое число в мире. G даже попало в Книгу рекордов Гиннеса. Последние 50 цифр числа Грэма выглядят так: …03222348723967018485186439059104575627262464195387.