Топ 10! универсальные законы логики + таблица!

Логические операции

Сложные логические суждения формируются из простых логических операций. Основные логические операции:

• конъюнкция или логическое умножение;
• дизъюнкция или логическое сложение;
• инверсия или логическое отрицание.

Конъюнкция

В основе логического умножения стоят два высказывания, в соответствие с которыми ставится новое суждение,  являющееся истиной лишь в том случае, когда оба исходных высказывания истинны.

Конъюнкция может быть записана следующими способами:

• A и B;
• A ⊥ B;
• A ⋅ B;
• A & B.

Пример

А – «Закончился дождь». B – «Из-за туч выглянуло солнце». Новое суждение «Закончился дождь, и из-за туч выглянуло солнце» является истиной только тогда, когда обе его части – А и B – истинны.

Дизъюнкция

При логическом сложении двух исходных суждений получается новое высказывание, ложное лишь в том случае, когда оба исходных суждения ложны.

Графическое обозначение дизъюнкции:

• A или B;
• A ⊦ B;
• A|B;
• A+B.

Пример

A – «В парке можно покататься на роликах»; B – «В парке можно просто погулять». Новое суждение «В парке можно покататься на роликах или просто погулять» будет ложным, есть и A, и B ложны.

Инверсия

При логическом отрицании в соответствие каждому суждению ставится противоположное исходному высказывание.

Символическое представление:

• не А;
• ¬А;
• Ā.

Пример

A – «За окном бушует вьюга». Ā – «Неверно, что за окном бушует вьюга».

Достаточное основание

Любое утверждение должно иметь основание. Это очевидно. Когда одна из сторон в споре утверждает что-либо, другая часто требует: «Обоснуй». Достаточным основанием при этом является достоверная информация. Любая истинная мысль должна быть обоснована в достаточной мере. Конечно, отсутствие достаточного основания не влечет ложности суждения, оно может быть истинным. Однако этот факт остается неизвестным до момента получения обоснования. При этом необходимо сказать, что в обосновании нуждается лишь истинное суждение. Ложное не может иметь достаточного основания вообще. Несмотря на то что в некоторых случаях с переменным успехом бывают попытки обосновать ложные суждения, такой подход нельзя назвать верным.

Закон достаточного основания не выражается в виде формулы, так как такой формулы нет.

Говоря, что достаточным основанием для суждения является истинная информация, мы имеем в виду различного рода данные, основанные на достоверных источниках. Для математики это цифровые выражения, выведенные без ошибок при помощи аксиом, теорем, различных систем, позволяющих осуществлять достоверные вычисления (такой системой, например, является таблица умножения). Достоверной будет считаться и информация, полученная на основе научных законов. Для обоснования нового суждения можно использовать выведенные ранее суждения, относительно которых доказано, что они истинны.

Закон достаточного основания, возможно, более чем любой другой действует в области повседневной жизни человека, а также применяется в рамках различных профессий. Это связано с тем, что в процессе познания человек прежде всего задумывается о том, на чем новая, полученная информация основана. Например, часто в СМИ можно услышать, что информация получена «из достоверных источников», или иногда применяется выражение «по непроверенным данным».

Конечно, закон непротиворечия и исключенного третьего, а также закон тожества играют огромную роль для правильного мышления. Однако они как бы следуют за законом достаточного основания. Потребность в них возникает, только когда происходит обоснование того или иного факта, понятия, суждения. Сказанное следует относить, конечно, не к научному значению законов логики, а, скорее, к необходимости этих законов для жизни и деятельности среднего человека.

В рамках данного вопроса необходимо сказать об одной особенности, характерной для логических основания и следствия при их соотношении с реальными основанием и следствием. Если в реальной жизни первым всегда идет основание, а из него выводится следствие, то в логике может иметь место обратная ситуация. Это связано с порядком вещей – в реальном мире сначала проходит процесс основания и только затем из него выводится следствие. Человек же, не имевший возможности наблюдать основание, может опираться только на следствие. Таким образом, получив следствие, человек умственно, виртуально может воссоздать основание.

Логика по Аристотелю

Древние греки вообще любили рассуждать о том, как устроен наш мир и в чём его смысл. У них это, кстати, получалось вполне неплохо. Так, учёный и философ Левкипп и его ученик Демокрит открыли атомы, не имея при этом наших микроскопов. Сделать это им удалось в том числе благодаря логике.

В Античности очень часто пользовались рассуждениями об объекте для его познания. Строился этот принцип на том, что во Вселенной есть законы, которые человек способен понять через мысли и опыт.

Вот и Аристотель был парень не промах. Он вывел четыре основных закона логики и определил, что это наука, которая является вспомогательной для познания мира. Она изучает законы и форму мышления, ведь только структурировавший своё мышление учёный будет способен совершать открытия.

Применение

В повседневной жизни

Любой наш знакомый изменяется с каждым годом, но мы всё же отличаем его от других знакомых и незнакомых нам людей (имеется возможность различения), потому что он сохраняет основные черты, которые выступают как те же самые на всём протяжении жизни нашего знакомого (имеется возможность отождествления). То есть, в соответствии с законом Лейбница (определяющим понятие тождество) мы утверждаем, что наш знакомый изменился. Однако в соответствии с законом тождества мы утверждаем, что это один и тот же человек, поскольку в основе определения лежит понятие личность. Закон тождества требует, чтобы для описания одного и того же понятия мы всегда использовали одно и то же выражение (имя). Таким образом, мы одновременно рассматриваем один объект (знакомого) на двух различных уровнях абстракции. Возможность различения и отождествления определяется в соответствии с законом достаточного основания. В данном случае в качестве достаточного основания используется наше чувственное восприятие (см. опознание).

В формальной логике

Под тождественностью мысли самой себе в формальной логике понимается тождественность её объёма. Это означает, что вместо логической переменной A{\displaystyle A} в формулу «A{\displaystyle A} есть A{\displaystyle A}» могут быть подставлены мысли различного конкретного содержания, если они имеют один и тот же объём.
Вместо первого A{\displaystyle A} в формуле «A{\displaystyle A} есть A{\displaystyle A}» мы можем подставить понятие «животное; обладающее мягкой мочкой уха», а вместо второго — понятие «животное, обладающее способностью производить орудия труда» (обе эти мысли с точки зрения формальной логики считаются равнозначными, неразличимыми, так как они имеют один и тот же объём, а именно — признаки, отражённые в этих понятиях, относятся лишь к классу людей), и при этом получается истинное суждение «Животное, обладающее мягкой мочкой уха, есть животное, обладающее способностью производить орудия труда».

В математике

В математической логике законом тождества называется тождественно истинная импликация логической переменной с самой собой X⇒X{\displaystyle X\Rightarrow X}.

В алгебре понятие арифметического равенства чисел рассматривается как особый случай общего понятия логического тождества. Однако имеются математики, которые, в противоположность данной точке зрения, не отождествляют символа «={\displaystyle =}», встречающегося в арифметике, с символом логического тождества; они не считают, что равные числа непременно тождественны, и поэтому рассматривают понятие числового равенства как специфически арифметическое понятие. То есть полагают, что сам факт наличия или отсутствия особого случая логического тождества, должен определяться в рамках логики..

Формы представления функций алгебры логики

Существует три способа представления выражений:

• в виде таблицы истинности;
• аналитическая форма;
• логическая форма.

Таблица истинности 

При этом способе комбинации логических переменных они расположены в порядке возрастания их двоичного номера. Наборы переменных обозначаются числами от нуля до 2n − 1, где n – количество переменных функции. При наличии значений на всех комбинациях функция называется полностью определенной.

Пример

Аналитическое выражение

Рассмотрение данной формы невозможно без введения новых понятий.

• терм – компонент выражения;
• ранг терма – число переменных в терме;
• дизъюнктивный терм (макстерм) – логическое сложение произвольного количества попарно независимых переменных;
• конъюнктивный терм (минтерм) – логическое умножение произвольного количества попарно независимых переменных. 

В аналитической записи используют две формы выражения:

дизъюнктивную нормальную форму (ДНФ)

\(f(a,b,c)=\overline ab\overline c+a\overline b+a\overline c+b\)

конъюнктивную нормальную форму (КНФ)

\(f(X_1X_2X_3X_4)=(X_1+\overline{X_2}+X_3)(\overline{X_1}+\overline{X_2}+X_3+X_4)(X_1+X_2)\)

При условии, что все термы, составляющие нормальную форму, имеют одинаковый и максимальный ранг, который равен количеству переменных функции, форма называется совершенной. В такой форме минтерм – конституентная единицы, макстерм – конституентная нуля.

Совершенная дизъюнктивная форма (дизъюнкция конституент единицы) записывается так:

\(F(a,b,c)=\overline abc+abc+abc+ab\overline c\)

Совершенная конъюнктивная форма (конъюнкция конституент нуля) имеет вид:

\(F(a,b,c,d)=(a+b+\overline c+d)(\overline a+b+\overline c+d)(\overline a+\overline d+\overline c+d)\)

Аналитические формы полностью дуальны.

Числовая запись

Данный вид записи функций алгебры логики позволяет представить ее компактно.

Вид для совершенной дизъюнктивной нормальной формы:

\(f(a,b,c)=\vee(1,3,6,7)\)

Вид для совершенной конъюнктивной нормальной формы:

\(f(a,b,c)=\wedge(0,2,4,5)\)

1.12.1. Гласные И, Ы, А, Я, У, Ю после шипящих Ж, Ш, Ч, Щ

Суждение

Суждение (или высказывание) – это форма мышления, в которой что-либо утверждается или отрицается. Например:

• Если человек читает, значит, он знает буквы.
• Любой ребенок нуждается в матери.
• Все собаки – это не кошки.
• Многие цветы приятно пахнут.

Давайте рассмотрим основные свойства суждения, чтобы понять, чем оно отличается от понятия.

1. Любое суждение состоит из связанных между собой понятий. Для примера возьмем два понятия – мужчина и женщина. Из них можно составить несколько суждений:

• мужчины и женщины – это люди;
• мужчины не являются женщинами;
• некоторые женщины сильнее мужчин.

1. Любое суждение выражается в форме предложения (в то время как понятие выражается словом). При этом не каждое предложение обязательно должно быть суждением.
2. Любое суждение является либо истинным, либо ложным. Если оно соответствует действительности, оно истинное, а если не соответствует – ложное.
3. Суждения бывают простыми и сложными. Сложные суждения состоят из простых, соединенных каким-либо союзом.

Из всего вышесказанного вытекает, что суждение представляет собой гораздо более сложную форму логического мышления, чем понятие. Именно поэтому в суждении выделяют четыре части: субъект, предикат, связку и квантор.

Не пугайтесь этих слов, они вовсе не так сложны, как кажется на первый взгляд. Кратко рассмотрим их.

Субъект (S) – это то, о чем идет речь в суждении. В суждении «Все растения не животные» речь идет о растениях, поэтому в данном случае субъектом являются растения.

Предикат (Р) – это то, что говорится о субъекте. В том же суждении «Все растения не животные» о субъекте «растения» говорится, что они – «не животные», поэтому предикатом данного суждения выступает понятие «животные».

Связка – это то, что соединяет субъект и предикат. Роль связки могут выполнять самые разные слова: есть, является, находится, это и т. п.

Квантор – это указатель на объем субъекта. В роли квантора могут быть слова все, некоторые, каждый пятый, половина, ни один и т. п.

Для закрепления давайте проанализируем простое суждение «Многие школьники любят физкультуру».

1. Субъект – «школьники»
2. Предикат – «физкультура»
3. Связка – «любят»
4. Квантор – «многие»

Надеемся, что это понятно. Стоит также отметить, что в некоторых суждениях квантор может отсутствовать. Однако он обязательно подразумевается. В суждении «Бабочки – это насекомые» квантор видимым образом отсутствует, но он подразумевается – это слово «все».

Вопросы в логике

Теперь давайте разберемся с тем, что такое вопрос, и почему его правильность так важна для логики.

Дело в том, что сам по себе вопрос очень близок к суждению. По сути, вопрос – это логическая форма, направленная на получение ответа в виде суждения.

Любой вопрос состоит из двух частей:

1. Основной (базисной), выраженной неким суждением (предпосылка вопроса);
2. Искомой, указывающей на необходимость дополнения этого суждения каким-то ответом.

С точки зрения логики одним из основных требований к постановке вопроса является истинность суждения базисной части. В противном случае вопрос считается логически некорректным.

Например, вопрос: «В каком году Достоевский написал «Войну и мир»?» следует признать логически некорректным, так как его базисная часть выражена ложным суждением «Достоевский написал «Войну и мир»».

3.2. Закон непротиворечия. Противоречащие суждения не могут бытьодновременно истинными или одновременно ложными.

Этот закон совпадает с отношением
противоречия по логическому квадрату
(речь идет о суждениях А – О, Е — I).

Пример: Все великие люди низкого
ростаА:ВсеSсутьР

Некоторые из великих людей не являются
людьми низкого роста. О:НекоторыеSне сутьР

По поводу закона непротиворечия
Аристотель утверждал: “… невозможно,
чтобы противоречащие утверждения были
вместе истинными”. Аристотель считал
этот закон наиболее важным принципом
не только мышления, но и самого бытия:“Невозможно, чтобы одно и то же вместе
было и не было присуще одному и тому же
и в одном и том же смысле”.Несколько
раньше формулировка закона как принципа
самого реального мира встречается у
Платона: “Невозможно быть и не быть
одним и тем же”. Суждение и его
отрицание должны говорить об одном и
том же предмете, в одном и том же отношении.

Являются
ли суждения А–Е противоречащими? Они
являются противоположными, так как не
могут быть одновременно истинными, но
могут быть одновременно ложными.

Все студенты пойдут в музей.
А: ВсеSсутьР

Ни один студент не пойдет в музей.
Е: Ни одно S не сутьР

Из двух противоречащих суждений одно
истинно, а второе – неизбежно ложно.
Если допускать противоречие в рассуждении,
то в итоге можно получить какой угодно
вывод.Человек может использовать
одно или другое суждение по ситуации,
т. е. отказаться от поисков истины и
исходных принципов нравственности.

Наличие или отсутствие противоречия
в рассуждениях являются свидетельством
уровня образованности и культуры
человека.

Особенность
противоречивости мышления часто
фиксируется в пословицах, поговорках.
Это факт свидетельствует о том, что
человек интересуется противоречием
мышления. Этот интерес является частью
нашей культуры, усваивается нами вместе
с языком общения.

Варианты противоречия:

• не украл, только взял;

• не били, а поколотили;

• не умер, а смерть его пришла;

• каждый из присутствующих размахивал
  руками энергичнее, чем его сосед;

• в связи с выездом за границу продаю
  редкую реликвию: череп Вольтера –
  ребенка;

• сеньор, немой явился … и хочет с вами
  поговорить;

• окружность со многими тупыми углами.

Следование закону непротиворечивости
мышления предполагает, что образованный
человек ставит перед собой задачу
логически корректного исследования
какой-либо проблемы или построения
доказательного обоснования определенной
точки зрения. Только в этой предметной
области имеет смысл говорить о применении
закона непротиворечивости и анализа
противоречия вообще.

Однако в тех сферах культуры, где не
ставится задача строгого следования
формально–логическим законам, не
корректно говорить об анализе противоречий
вообще. Такой сферой культуры может
быть, например, художественная литература.
Поэтому писатель свободно может допускать
высказывания типа:

• жениться стоит и не стоит;

• осень настала и еще не настала;

• как говорит статистика, замужних женщин
  заметно больше, чем женатых мужчин: при
  переписи анкета заполняется со слов
  самого опрашиваемого.

Замечание к данному высказыванию “при
переписи анкета заполняется со слов
самого опрашиваемого” настраивает на
мысль о том, что правдивых ответов не
было ни у мужчин, ни у женщин – женщины,
наверняка, более скрывали свое
незамужество, чем мужчины, а мужчины,
возможно, будучи женаты, при опросе это
отрицали, что и привело к противоречивому
высказыванию “… замужних женщин заметно
больше, чем женатых мужчин”

Для читателя интуитивно ясно, о чем идет
речь. С формально-логической же точки
зрения о наличии или отсутствии
противоречий в выше предложенных
высказываниях вообще говорить нет
смысла.

Противоречие недопустимо в строгом
рассуждении, когда оно смешивает истину
с ложью.Но у противоречия в обычном
языке много разных задач. Оно может
выступать в качестве основного сюжета
какого-нибудь рассказа, быть средством
достижения особой художественной
выразительности.

“Да! Ненавижу и вместе люблю. – Как
возможно, ты спросишь? Не объясню я. Но
так чувствую, смертно томясь”. (1 в. до
н. э., рим. Поэт Катулл)

Все мы полны противоречий. Каждый из
нас – просто случайная мешанина
несовместимых качеств. “… Человек
знает, что хорошо, но делает то, что
плохо”, — с горечью замечал Сократ.

3.3.На первый взгляд самым простым
из логических законов, соответствующим
последовательности рассуждений является
закон тождества.

Закон тождества. Определенное
утверждение должно сохраняться на
протяжении определенного рассуждения,
не изменяясь ни по количеству, ни по
качеству.

Ход урока

1. Организационный момент.

Цель: подготовить учащихся к уроку.

Объявляется тема урока. Перед учащимися ставится задача: показать, как они научились решать задачи по теме.

2. Повторение изученного материала.

Выполнение в тестирующей оболочке MyTest теста на тему «Основные понятия алгебры логики».(приложение1.mtf)

3. Изучение нового материала.

Вопросы для изучения:

1. Простые и сложные выражения.
2. Основные логические операции.

При объяснении нового материала используется компьютерная презентация (презентация.PPT)

1. Простые и сложные выражения.

Логические выражения могут быть простыми и сложными.

Простое логическое выражение состоит из одного высказывания и не содержит логические операции. В простом логическом выражении возможно только два результата — либо «истина», либо «ложь».

Сложное логическое выражение содержит высказывания, объединенные логическими операциями. По аналогии с понятием функции в алгебре сложное логическое выражение содержит аргументы, которыми являются высказывания.

2. Основные логические операции.

По ходу объяснения нового материала ученики заполняют в тетради таблицу следующего вида.

Название логической операции	Обозначение логической операции	Результат выполнения логической операции	Таблица истинности	Примеры
Отрицание
Дизъюнкция
Конъюнкция
Импликация
Эквиваленция

В качестве основных логических операций в сложных логических выражениях используются следующие:

• НЕ (логическое отрицание, инверсия);
• ИЛИ (логическое сложение, дизъюнкция);
• И (логическое умножение, конъюнкция)

Операция НЕ — логическое отрицание (инверсия)

Логическая операция НЕ применяется к одному аргументу, в качестве которого может быть и простое, и сложное логическое выражение. Результатом операции НЕ является следующее:

• если исходное выражение истинно, то результат его отрицания будет ложным;
• если исходное выражение ложно, то результат его отрицания будет истинным.

Для операции отрицания НЕ приняты следующие условные обозначения: НЕ, ‾, ˥ not А. Результат операции отрицания НЕ определяется следующей таблицей истинности.

Операция ИЛИ — логическое сложение (дизъюнкция, объединение)

Логическая операция ИЛИ выполняет функцию объединения двух высказываний, в качестве которых может быть и простое, и сложное логическое выражение. Высказывания, являющиеся исходными для логической операции, называют аргументами.

Результатом операции ИЛИ является выражение, которое будет истинным тогда и только тогда, когда истинно будет хотя бы одно из исходных выражений.

Результат операции ИЛИ определяется следующей таблицей истинности:

А	В	A v В
1	1
1	1
1	1	1

Применяемые обозначения: А или В; A v В; А ог В. При выполнении сложных логических преобразований для наглядности условимся пользоваться обозначением А + В, где А, В — аргументы (исходные высказывания).

Операция И — логическое умножение (конъюнкция)

Логическая операция И выполняет функцию пересечения двух высказываний (аргументов), в качестве которых может быть и простое, и сложное логическое выражение.

Результатом операции И является выражение, которое будет истинным тогда и только тогда, когда истинны оба исходных выражения.

Результат операции И определяется следующей таблицей истинности:

А	В	А^ В
1
1
1	1	1

Применяемые обозначения: А и В; А ^ В; А & В; A and В.

Условимся пользоваться при выполнении сложных логических преобразований обозначением A-В, где А, В — аргументы (исходные высказывания).

Операция «ЕСЛИ-TO— логическое следование (импликация)

Эта операция связывает два простых логических выражения, из которых первое является условием, а второе — следствием из этого условия.

Применяемые обозначения:

если А, то В; А влечет В; if A then В; А—»В.

Результат операции следования (импликации) ложен, только тогда, когда предпосылка А истинна, а заключение В (следствие) ложно.

Таблица истинности:

А	В	Если А, то В
1
1	1
1
1	1	1

Операция «А тогда и только тогда, когда В» (эквивалентность, равнозначность)

Применяемое обозначение: А ~В.

Результат операции эквивалентность истинен только тогда, когда А и В одновременно истинны или одновременно ложны.

Таблица истинности:

А	В	А ~ В
1
1	1
1
1	1	1

4. Закрепление изученного материала

5. Подведение итогов урока

Скажите был ли сегодняшний урок для вас познавательный?

Что больше всего запомнилось из урока?

6. Домашнее задание

1. Учебник. п.23.2., заполнить таблицу «Логические операции» до конца.
2. Выполнить задание (приложение 3)
3. Подготовиться к тестированию.
4. Знать ответы на вопросы:
   • какие высказывания бывают;
   • какие высказывания называются простыми, а какие – сложными;
   • основные логические операции и их свойства.

Законы логики

Как и в любой науке, здесь существуют определенные правила. Закон логики – это принцип, которому необходимо следовать, чтобы из истинных суждений получить правильный вывод. Их разработал и сформулировал еще Аристотель, изучая формальную логику, в которой использовались словесные суждения. Существует четыре базовых закона, нарушение которых приводит к появлению умышленных или неумышленных ложных выводов:

• тождества;
• непротиворечия;
• исключенного третьего;
• достаточного основания.

Закон тождества

Изучая, что такое наука логика, непременно сталкиваются с ее первым законом тождества или равенства. Некоторые именуют его принципом постоянства. Суть состоит в том, что на всем протяжении логического рассуждения изначальное понятие должно сохранять свой первоначальный смысл. Искажение, которое свойственно многим языкам и двойственность, многозначность, могут привести к ложным выводам.

Примером несоблюдения этого принципа является простой диалог:

• Зачем чай в кружке?
• Очевидно же! Чтобы его кто-то выпил!
• Нет. Чай в кружке за ее стенкой. То есть здесь было подменено понятие слов зачем и за чем, сделан ложный вывод.

Закон непротиворечия

Еще одним фундаментальным постулатом является закон непротиворечия. Его суть состоит в том, что два противоположных высказывания не могут быть одновременно истинными. Одно или оба из них обязательно окажутся ложными. Можно привести простой пример иллюстрации этого закона:

1. Маша утверждает, что абрикос из корзинки взяла Таня.
2. Таня же опровергает сестру и уверена, что абрикос взяла Маша.
3. Два противоположных суждения не могут быть одновременно истинными. То есть либо Таня взяла абрикос, и Маша права, либо наоборот.
4. Оба эти выражения могут быть ложными, если абрикос просто упал из корзинки и закатился под стол, потому как емкость была переполнена.

Закон исключенного третьего

Нередко студенты изучая, что такое наука логика, путают предыдущий закон с принципом исключенного третьего. Они схожи, но суть каждого все же отличится. Этот закон сформулирован так, что истинным может быть либо само суждение, либо же его отрицание. Третьего не дано. То есть закон оперирует не противоположными понятиями, а противоречащими друг другу. К примеру:

1. Утверждение «все голуби – птицы» – верно.
2. Ему противоречит вывод, что все голуби – не птицы. Или «не все голуби – птицы». Вторые высказывания ложны. Третьего высказывания быть не может.

Закон достаточного основания

Четвертый закон – логического мышления, был сформулирован не Аристотелем, а лишь в XVIII в. озвучен Готфридом Лейбницем. Суть принципа состоит в том, что любой тезис будет иметь силу только тогда, когда будет подтвержден аргументами. Причем они должны быть такими, чтобы исходная мысль четко вытекала из них.

Самым ярким и знаменитым примером применения закона достаточного основания в жизни является принцип так называемой презумпции невиновности:

1. Ее суть состоит в том, что любой человек не считается виновным до тех пор, пока совершение им преступления не доказано фактами.
2. Даже если заключенный дает показания против себя – это не является веским фактом признания его виновным.
3. Для доказательства обвинителю необходимо привести прямые улики и достоверные факты участия обвиняемого в совершении преступления.

Функциональные схемы

Сигнал, который вырабатывает один логический элемент, можно подать на вход другого элемента. Это даст возможность образовать цепочку из отдельных логических элементов – функциональную схему.

Пример 1

Функциональная (логическая) схема – это схема, которая выполняет определённую функцию и состоит из базовых логических элементов. Проанализировав фунциональную схему, можно понять, как работает логическое устройство, то есть ответить на вопрос, какую же функцию она выполняет. А чтобы описать функциональную схему, нужна структурная формула.

Как по заданной функциональной схеме записать структурную формулу?

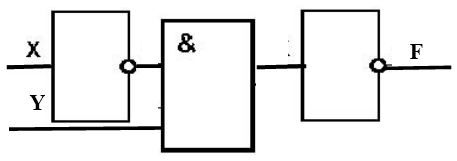Рисунок 6.

Элемент И осуществляет конъюнкцию $\bar{X}$ и $Y$, над результатом в элементе НЕ выполняется операция отрицания, то есть вычисляется значение выражения

Рисунок 7.

Записали, что структурной формулой данной функциональной схемы является формула

Рисунок 8.

Для функциональной схемы нужно составить таблицу значений сигналов на входах и выходах схемы, по которой можно понять, какую функцию выполняет данная схема, – таблицу истинности.

Составим таблицу истинности для вышеприведённой схемы. Количество столбцов таблицы равно суммарному количеству входов и выходов нужной схемы. Итого $5$ столбцов. Количество строк таблицы равно $2^n$, где $n$ – количество входов (здесь два), строк $4$.

Рисунок 9.

Обработка любой информации на компьютере − выполнение процессором различных арифметических и логических операций. Для этого в составе процессора есть арифметико-логическое устройство (АЛУ), которое состоит из ряда устройств, построенных на логических элементах, рассмотренных выше. Главными устройствами являются триггеры, полусумматоры, сумматоры, шифраторы, дешифраторы, счетчики, регистры.

Конструируется логическое устройство по следующему алгоритму:

1. по заданным условиям работы проектируемого узла (т.е. по соответствию его входных и выходных сигналов) строится таблица истинности;
2. конструируется логическая функция данного узла по таблице истинности, выполняется при необходимости её преобразование (упрощение), если cоставляется функциональная схема проектируемого узла по формуле логической функции;
3. реализуется полученная схема.