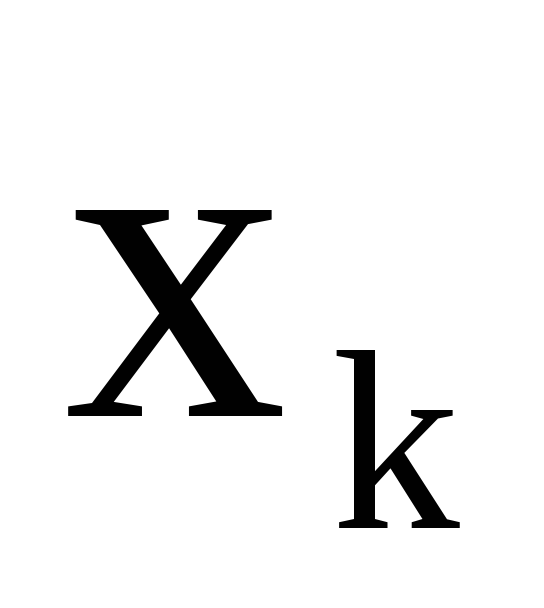Значение слова «приближенный»

Содержание:

Приближенные вычисления с помощью правил подсчета цифр
Оценка погрешности и точность вычисления
Бизнес и финансы
Правила вычислений с приближенными числами
Слайды и текст этой презентации
Справочная информация
Класс точности и его использование для оценки инструментальной погрешности приборов
Справочная информация
Sin 0.5
Погрешности вычислений
4.5. Дифференцирование сложной функции
Справочная информация
В словаре Д.Н. Ушакова
В словаре Полная акцентуированная парадигма по А. А. Зализня
Бизнес и финансы
Приближенное вычисление определенных интегралов
Справочная информация
История

Приближенные вычисления с помощью правил подсчета цифр

I. При сложении и
вычитании приближенных чисел в результате
следует сохранять столько десятичных
знаков, сколько их в приближенном, данном
с наименьшим числом десятичных знаков.

Пример.
Найти сумму приближенных чисел 127,42;
67,3; 0,12 и 3,03.

Решение:
127,42 + 67,3 + 0,12 + 3,03 = 197,87
197,9

Пример.
Найти разность чисел: 418,7 — 39,832 = 378,868
378,9

II.
При умножении и делении приближенных
чисел в произведении надо сохранить
столько значащих цифр, сколько их есть
в данном числе с наименьшим количеством
значащих цифр.

Пример.
Умножить приближенные числа 3,4 и 12,32.

Решение:
3,4 х 12,32 = 41,888
42

Задача.
Площадь прямоугольной грядки приближенно
равна 7,6 кв. м, ширина -2,38 м. Чему равна
ее длина?

Решение.
Длина грядки равна частному от деления
7,6 на 2,38.

Действие
деления выполняют так: 7,60 : 2,38 = 3,19
3,2(м)

Последнюю
цифру частного 9 можно было и не писать,
а, получив в частном две значащие цифры,
заметив, что остаток больший половины
делителя, округлить частное с избытком.

III.
При возведении приближенных чисел в
квадрат, и куб в результате сохраняется
столько значащих цифр, сколько их в
основании.

Примеры.

2,32 =
5,29 ≈ 5,3;

0,83 =
0,512 ≈ 0,5.

IV.
В промежуточных результатах следует
брать одной цифрой больше, чем рекомендуют
предыдущие правила.

V.
Если некоторые данные имеют больше
десятичных знаков (при действиях первой
ступени) или больше значащих цифр (при
действиях II
и III
ступеней), чем другие, то их предварительно
следует округлить, сохраняя лишь одну
запасную цифру.

VI.
Если данные можно брать с произвольной
точностью, то для получения результата
с k цифрами
данные следует брать с таким числом
цифр, которое дает согласно правилам I
— IV k +
1 цифру в результате.

3.
Применение правил.Применение
вычислений способом подсчета цифр
рассмотрим на примере.

Пример.
Найти значение ,
если а≈
9,31, b ≈
3,1, с≈
2,33.

Решение.

а— b =
9,31 — 3,1 = 6,21;

(а— b ) с=
6,21 · 2,33 ≈ 14,5;

а+ b =
9,31 + 3,1 = 12,4;

х=
14,5 : 12,4 ≈ 1,2.

Ответ. х≈
1,2.

Примечание.
Сформулированные выше правила подсчета
цифр имеют вероятностный смысл: они
наиболее вероятны, хотя существуют
примеры, не удовлетворяющие этим
правилам. Поэтому вычисления способом
подсчета цифр — самый грубый способ
оценки погрешности результатов действий.
Однако он очень прост и удобен, а точность
таких вычислений вполне достаточна для
большинства технических расчетов.
Поэтому этот способ широко распространен
в вычислительной практике.

В более
ответственных вычислениях пользуются
способом границ или способом граничных
погрешностей.

Оценка погрешности и точность вычисления

Значение слова «спросить»

Погрешность
приближенного вычисления интегралов
состоит из остаточного члена квадратурной
формулы и различных погрешностей
округления.

На
практике для оценки остаточного члена
вычисляют два значения интеграла.

при
разбиении интервала интегрирования на
n
частей и применяют правило Рунге:

для
формул прямоугольников и трапеций,

для
формулы Симпсона.
(5)

Здесь

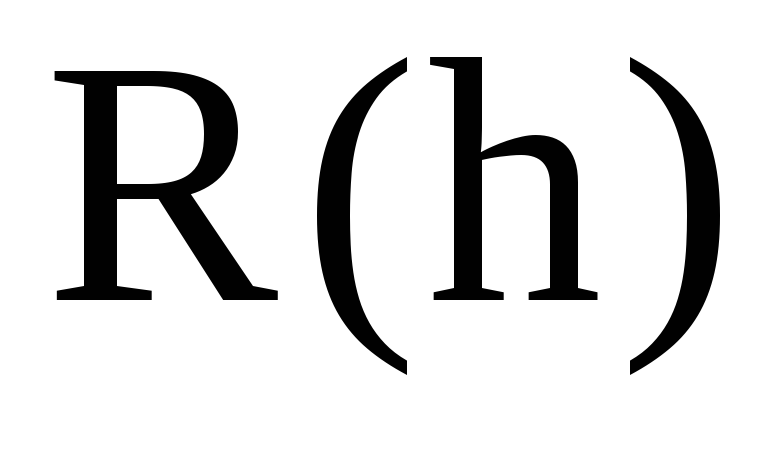— остаточный член (погрешность) более
точного значения интеграла.

Чтобы
погасить погрешность округления,
промежуточные вычисления проводят с
одним запасным знаком.

При
одном и том же числе разбиений наибольшую
точность дает метод Симпсона.

Пусть

— заданная точность вычислений, тогда
выбираютn
таким, чтобы

—
для формул прямоугольников и трапеций,

—
для формулы Симпсона.
(6)

Причём
для формул Симпсона
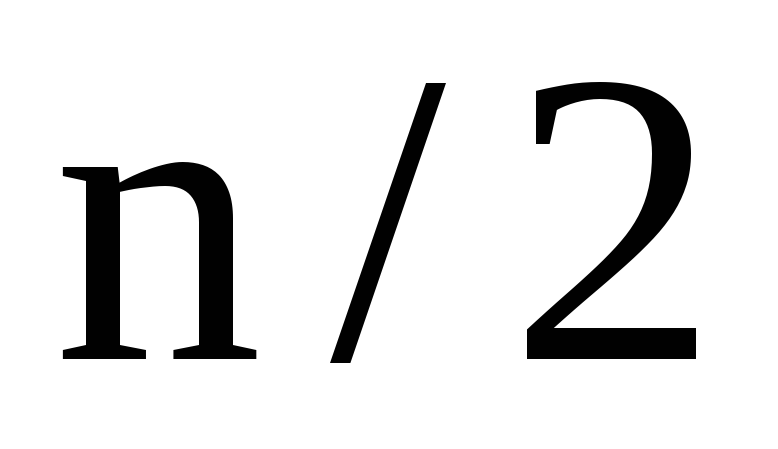должно быть обязательно целым, т. е.

и
т. п.

Пример.
Вычислить
интеграл
с точностьюметодом Симпсона.

Решение.
Вычисление интеграла проводить по
следующему плану

Выбрать
шаг интегрирования. Здесь можно взять
n
= 16 и h
= 0,125.
Определить
узлы сетки:

3.
Для каждого
вычислить значение подынтегральной
функции

и
записать в один из трех столбцов
бланка расчета в зависимости от номера
k

(табл.
1).

Вычислить
значение интеграла
по формуле (4).
Для
оценки погрешности вычислить

Заметим,
что для этого нужно использовать значение
функции только в четных узлах.

Определить
значение
Если

,
то записать в качестве ответа

В
противном случае следует повысить
точность вычислений одним из двух
способов

1.
Правило Рунге: если известны два значения
интеграла
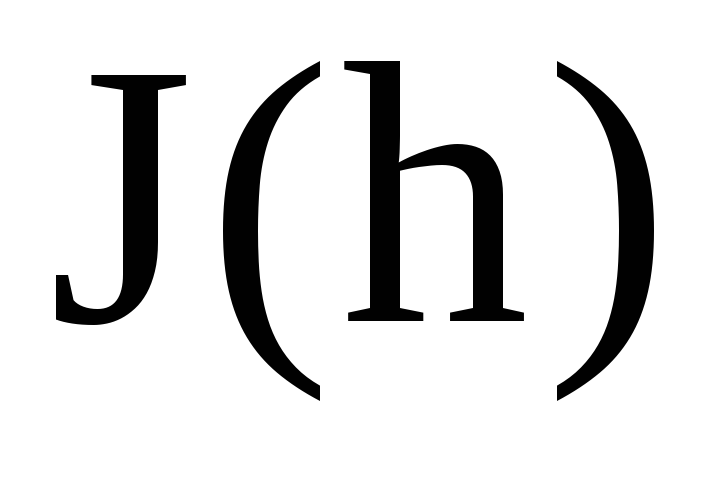и,
то очень хорошую точность можно получить,
если к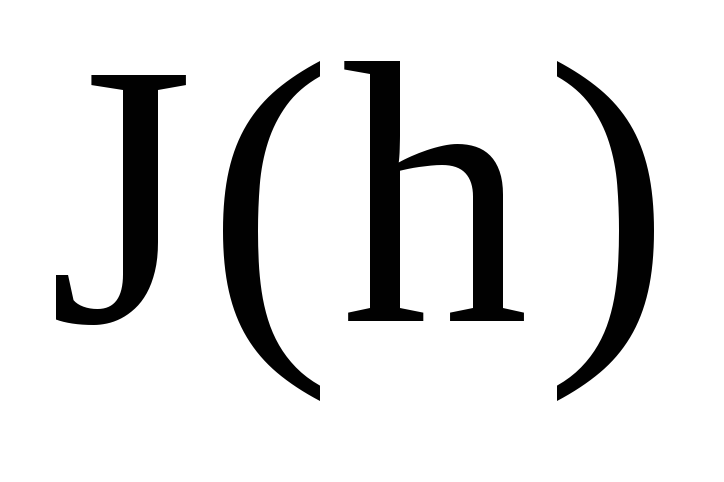прибавить величину погрешности,
найденную по формуле Рунге:

—
для методов прямоугольников и трапеций,

—
для метода Симпсона.
(7)

2.
Способ двойного пересчета: увеличим
число разбиений n
вдвое по сравнению с тем, при котором
вычисляли
,
и найдем новое значение интеграла,
если потребуется, то будем уменьшать
шаг сетки до тех пор, пока не будут
выполняться неравенства

где

— заданная точность.

Таблица
1



Номера узлов k	Узлы
k=0; k=16	k — четные	k — нечетные
0,5	0)- 0,69315
1	0,625			— 0,47000
2	0,750		1) – 0,28768
3	0,875			— 0,13353
4	1,000		2) 0,00000
5	1,125			0,11778
6	1,250		3) 0,22315
7	1,375			0,31845
8	1,500		4) 0,40546
9	1,625			0,48551
10	1,750		5) 0,55962
11	1,875			0,62861
12	2,000		6) 0,69315
13	2,125			0,75377
14	2,250		7) 0,81093
15	2,375			0,86500
16	2,500	8) 0,91629
Суммы n=16 n=8	0,22314	2,40463	2,56559
0,22314
Интегралы
Погрешность
Ответ

Бизнес и финансы

Значение слова «определить»

БанкиБогатство и благосостояниеКоррупция(Преступность)МаркетингМенеджментИнвестицииЦенные бумагиУправлениеОткрытые акционерные обществаПроектыДокументыЦенные бумаги — контрольЦенные бумаги — оценкиОблигацииДолгиВалютаНедвижимость(Аренда)ПрофессииРаботаТорговляУслугиФинансыСтрахованиеБюджетФинансовые услугиКредитыКомпанииГосударственные предприятияЭкономикаМакроэкономикаМикроэкономикаНалогиАудитМеталлургияНефтьСельское хозяйствоЭнергетикаАрхитектураИнтерьерПолы и перекрытияПроцесс строительстваСтроительные материалыТеплоизоляцияЭкстерьерОрганизация и управление производством

Правила вычислений с приближенными числами

Значение слова «литературный»
Результат
суммирования (вычитания) приближенных
чисел будет иметь столько верных знаков,
сколько их имеет слагаемое с наименьшим
числом верных знаков.
При
умножении (делении) в полученном
результате будет столько значащих
верных цифр, сколько их в исходном числе
с наименьшим количеством верных знаков.
При
возведении в степень (извлечении корня)
любой степени результат имеет столько
же верных знаков, сколько их в основании.
Число
и мантисса его логарифма содержит
одинаковое количество верных знаков.
Правило
запасной цифры.
Чтобы по возможности уменьшить ошибки
округления, рекомендуется в тех исходных
данных, которые это позволяют, а также
и в результате, если он будет участвовать
в дальнейших вычислениях, сохранить
по одной лишней цифре сверх того, что
определено правилами 1-4.

Слайды и текст этой презентации

Слайд 1

Текст слайда:

Практические приемы приближенных вычислений.

А-8 урок 1

Слайд 2

Текст слайда:

Стандартный вид числа.

Слайд 3

Текст слайда:

Если с – натуральное число или положительная конечная десятичная дробь, то представление этого числа в видес = а∙10nгде 1≤а˂10, k-целое число, называют записью числа в стандартном виде.а- мантисса числаk-порядок числа с

Стандартный вид числа.

Слайд 4

Текст слайда:

520=5,2∙1020,0054=5,4∙10-323000=2,3∙104123456789=1,23456789∙108

Стандартный вид числа.

Слайд 5

Текст слайда:

Назовите правильную запись числа в стандартном виде:

0,00000123 =

Слайд 6

Текст слайда:

Назовите правильную запись числа в стандартном виде:

0,000512 =

Слайд 7

Текст слайда:

Назовите правильную запись числа в стандартном виде:

830000000 =

Слайд 8

Текст слайда:

Назовите правильную запись числа в стандартном виде:

456000 =

Слайд 9

Текст слайда:

Назовите число, записанное в стандартном виде:

Правильный ответ

Слайд 10

Текст слайда:

Верные и сомнительные цифры

Цифру какого-либо разряда в записи приближенного значения называют верной, если граница абсолютной погрешности не превосходит единицы этого разряда. В противном случае цифру называют сомнительной.

Если граница абсолютной погрешности не превосходит половины единицы разряда, следующего за разрядомрассматриваемой цифры, то эту цифру в записи приближенного значения числа называют строго верной.

Слайд 11

Текст слайда:

№ 239(2,4,6)

№ 240 (2,4,6)

Слайд 12

Текст слайда:

Сложение и вычитание приближенных значений .

Теорема: Границы абсолютных погрешностей суммы и разности приближенных значений равны сумме границ абсолютных погрешностей каждого из приближений.

х = а + h1

y = b + h2

х + y = (а + b) + (h1 + h2)

x — y = (а — b) + (h1 + h2)

Слайд 13

Текст слайда:

При сложении и вычитании приближенных значений, в записи которых все цифры верные, в сумме и в разности оставляют столько десятичных знаков, сколько их имеет приближенное значение с наименьшим числом десятичных знаков.

Слайд 14

Текст слайда:

№ 241(2,4,6)

Слайд 15

Текст слайда:

Умножение и деление приближенных значений.

Значащими цифрами называются все верные цифры в десятичной записи приближенного значения, кроме нулей, стоящих перед первой отличной от нуля цифрой.

0,025

1230

0,00350

Слайд 16

Текст слайда:

Умножение и деление приближенных значений.

При умножении и делении приближенных значений в произведении и частном оставляют столько цифр ( не считая нулей, отличной от нуля цифрой) , сколько значащих цифр имеет приближенное значение с меньшим числом значащих цифр.

Справочная информация

ДокументыЗаконыИзвещенияУтверждения документовДоговораЗапросы предложенийТехнические заданияПланы развитияДокументоведениеАналитикаМероприятияКонкурсыИтогиАдминистрации городовПриказыКонтрактыВыполнение работПротоколы рассмотрения заявокАукционыПроектыПротоколыБюджетные организацииМуниципалитетыРайоныОбразованияПрограммыОтчетыпо упоминаниямДокументная базаЦенные бумагиПоложенияФинансовые документыПостановленияРубрикатор по темамФинансыгорода Российской Федерациирегионыпо точным датамРегламентыТерминыНаучная терминологияФинансоваяЭкономическаяВремяДаты2015 год2016 годДокументы в финансовой сферев инвестиционной

Класс точности и его использование для оценки инструментальной погрешности приборов

Класс
точности – обобщенная характеристика,
используемая для оценки предельных
значений основной и дополнительной
погрешностей.

Основной
называют погрешность прибора, присущую
ему в нормальных условиях эксплуатации.

Условия
эксплуатации определяются значениями
влияющих на показания приборов величин,
не являющихся для данного прибора
информативными. К влияющим величинам
относят температуру среды, в которой
выполняются измерения, положение шкалы
прибора, частоту измеряемой величины
(не для частотомеров), напряженность
внешнего магнитного (или электрического)
поля, напряжение питания электронных
и цифровых приборов и др.

В
технической документации прибора
указывают нормальный и рабочий диапазоны
значений влияющих величин. Использование
прибора при значении влияющей величины
вне пределов рабочего диапазона не
допускается.

Класс
точности прибора устанавливают по
форме:

предела
абсолютной погрешности
Δ_пр
= ± а или Δ_пр
= ± (а + b
• A);
предела
относительной погрешности
δ_пр
= ± p
или δ_пр
= ± [c
+ d((A_max/A)-1)];
предела
приведенной погрешности
γ_пр
= ± k

Числа
a,
b,
p,
c,
d,
k
выбирают из ряда 1; 1,5; 2; 2,5; 4; 5; 6•10n,
где n
= 1, 0, -1, -2 и т.д.

А
– показания прибора;

А_max
– верхний предел используемого диапазона
измерений прибора.

Приведенная
погрешность

где
А_н
– нормирующее значение, условно принятое
для данного прибора, зависящее от формы
шкалы.

Определение
А_н
для наиболее часто встречающихся шкал
приведены ниже:

а)
односторонняя шкала б) шкала с нулем
внутри

А_н
= А_max
A_н
= |A₁|
+ A₂

в)
шкала без нуля г) существенно
неравномерная шкала
(для омметров, фазометров)

А_н
= А₂
– А₁А_н
= L

Правила
и примеры обозначения классов точности
приведены в таблице 3.1.

Таблица
3.1

Формула
для предельной основной погрешности

Обозначение
класса точности на приборе

общий
вид

пример

Δ
= ± а

Δ
= ± (а
+ b • A)

±
а, ед. величины А

±
(а + b
• A),
ед. величины А

Римскими
или латинскими буквами

δ
= (100•Δ)/A
=
± p

δ
= [c+d(A_max/A-1)]

±
p,
%

±[c+d(A_max/A-1)],
%

c/d

1,5

1,0/0,5

γ
= (100•Δ)/A_н
= ± k

если
А_н
= L_шк,
то

γ
= (100•Δ´)/L_шк
=±
k

±
k,
%

1,5

Пределы
допускаемых дополнительных погрешностей
устанавливают в виде: а) постоянного
значения для рабочего диапазона влияющей
величины;

б)
отношения предела допускаемой
дополнительной погрешности, соответствующего
регламентированному интервалу влияющей
величины, к этому интервалу;

в)
предельной функции влияния и др.

Справочная информация

Sin 0.5

Погрешности вычислений

Пусть нужно вычислить площадь сечения цилиндра, диаметр которого D — 1,2 см известен с точностью 0,1 см. По известной формуле площади круга получаем (например, на калькуляторе):

Рис. 9.2

Значит ли это, что мы нашли площадь с такой точностью? Конечно, нет. Вспомним, что диаметр был измерен с точностью 0,1 см, т. е. он мог быть в самом деле равен как 1,1 см, так и 1,3 см. В этих «крайних» случаях получаем площадь

Таким образом, следует записать ответ в виде S ≈ 1,1 ± 0,2 см2.

Относительную погрешность результата можно оценить как

Заметим, что мы не учитывали погрешность, связанную с неточностью задания иррационального числа π.

Все практические расчёты выполняются неточно. Погрешность результата вычислений определяется в первую очередь погрешностью исходных данных.

Теперь вернёмся к расчётам с помощью компьютера. Как вы знаете из главы 4, данные записываются в память в двоичном коде ограниченной длины, при этом практически все вещественные числа хранятся неточно. При выполнении вычислений погрешности накапливаются, поэтому при сложных расчётах может получиться неверный ответ. Например, с точки зрения точности очень плохо, если ответ — это небольшое (по модулю) число, которое вычисляется как разность двух неточных больших чисел (вспомните пример с кружкой!).

Погрешность резко возрастает при делении на неточное малое по модулю число. Предположим, что нужно вычислить значение

причём а, b, с и d — вещественные числа, которые получены в результате вычислений с погрешностью 0,001: a = 1000 ± 0,001; b = 0,002 ± 0,001; с = 1000 ± 0,001; d = 0,003 ± 0,001.

Легко проверить, что вычисленное значение х может находиться в интервале от -166 667 до 750 001, т. е. относительная погрешность превышает 300%! Такой метод расчётов вычислительно неустойчив: малые погрешности в исходных данных могут привести к огромным погрешностям в решении.

Подводя итог, можно выделить несколько источников погрешностей при компьютерных вычислениях:• неточность исходных данных;
• неточность записи вещественных чисел в двоичном коде конечной длины;
• погрешности приближённого вычисления некоторых стандартных функций (например, sin(x) или cos(x));
• накопление погрешностей при арифметических действиях с неточными данными;
• собственная погрешность используемого метода (для приближённых методов, рассматриваемых в следующем параграфе).

Проблемы, возникающие при вычислениях с конечной точностью, изучает вычислительная математика, задача которой — разработать вычислительно устойчивые методы решения задач, при которых небольшие погрешности исходных данных мало влияют на результат. Иногда этого удаётся добиться простым изменением порядка действий или преобразованием формул.

Следующая страница Вопросы и задания

Cкачать материалы урока

4.5. Дифференцирование сложной функции

ТЕОРЕМА
3.
Пусть функция х =
φ(t)
имеет производную в точке
t,
а функция у =
f(x)
имеет производную в соответствующей
точке
x
= φ(t).
Тогда сложная функция
f[φ(t)]имеет
производную в точке
t
u
справедлива следующая формула:

В теореме 4.3
рассмотрена суперпозиция двух функций,
где у
зависит от t
через промежуточную переменную х.
Возможна и более сложная зависимость
с двумя и более промежуточными
переменными, однако правило
дифференцирования сложной функции
остается тем же. Например, если у
= у(х), х = φ(и), и =
ψ(t),
то производная
y'(t)
вычисляется по формуле

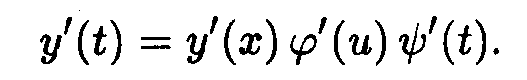
Рассмотрим
несколько примеров на дифференцирование
сложной функции.

Пример 1.
Найти производную функции у
=
tg (x3).

Решение.
Эту функцию можно представить через
промежуточную переменную и
как y
=tg
u, и =
х3.
Тогда по формуле (4.7) имеем

Пример 2.
Найти производную функции у
=
.

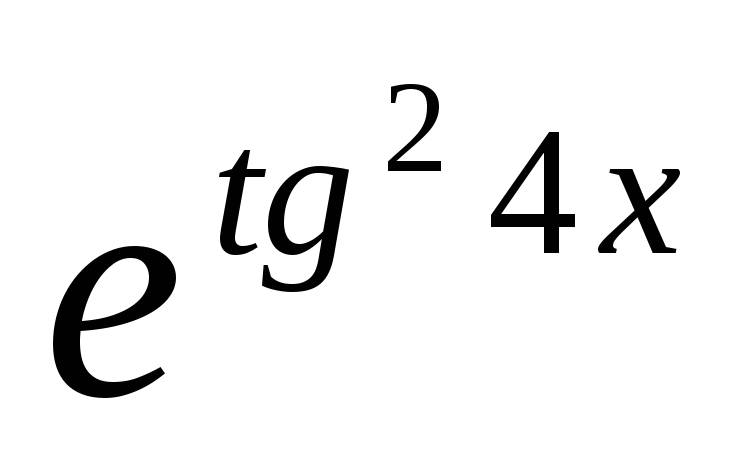Решение.
Здесь функция представляется с помощью
трех промежуточных переменных: у
= еu,
и =
v2,
v
= tg
w, w =
4x.
Применяя правило (4.7) дифференцирования
сложной функции, последовательно
получаем

Пример 3.
Найти угол наклона к оси Оx
касательной
к графику функции

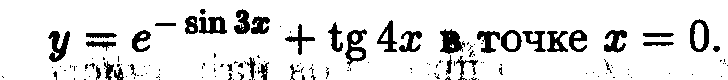
Решение.
Данная функция является суммой двух
сложных функций, представляемых через
промежуточные переменные как

Применяя правила
дифференцирования суммы функций и
сложных функций, получаем

Поскольку тангенс
угла наклона касательной к оси Ох
при х =
0 равен значению производной в этой
точке, из последнего равенства получаем,
подставляя в него х
= 0:

откуда φ
=
arctg 1 = 45°.

Справочная информация

В словаре Д.Н. Ушакова

ПРИБЛИ́ЖЕННЫЙ, приближенная, приближенное; приближен, приближена, приближено (·книж. ). прич. страд. прош. вр. от приблизить» title=’что такое приблизить, значение слова приблизить в словаре Ушакова’>приблизить и от приближать» title=’что такое приближать, значение слова приближать в словаре Ушакова’>приближать. «Беда стране, где раб и льстец одни приближены к престолу.» Пушкин.II. ПРИБЛИЖЁННЫЙ, приближённая, приближённое (·книж. ).1. Пользующийся чьим-нибудь преимущественным доверием, состоящий в числе близких лиц, окружающих кого-нибудь (·устар. ).| То же, в знач. сущ. приближённый, приближённого, ·муж., приближённая, приближённой, ·жен. (·устар. ). Царь со своими приближенными.2. Не совсем точный, но приблизительно совпадающий с истинным, близкий к истинному (мат.). Приближенное значение какой-нибудь величины (разнящееся от истинного на его величины или менее того). Приближенное вычисление. Приближённый результат.

В словаре Полная акцентуированная парадигма по А. А. Зализня

1. приближённый,приближённая,приближённое,приближённые,приближённого,приближённой,приближённого,приближённых,приближённому,приближённой,приближённому,приближённым,приближённый,приближённую,приближённое,приближённые,приближённого,приближённую,приближённое,приближённых,приближённым,приближённой,приближённою,приближённым,приближёнными,приближённом,приближённой,приближённом,приближённых,приближён,приближённа,приближённо,приближённы,приближённее,поприближённее,приближённей,поприближённей2. приближённый,приближённые,приближённого,приближённых,приближённому,приближённым,приближённого,приближённых,приближённым,приближёнными,приближённом,приближённых

Бизнес и финансы

Приближенное вычисление определенных интегралов

Пусть
требуется найти определенный интеграл

гденепрерывна на отрезке.

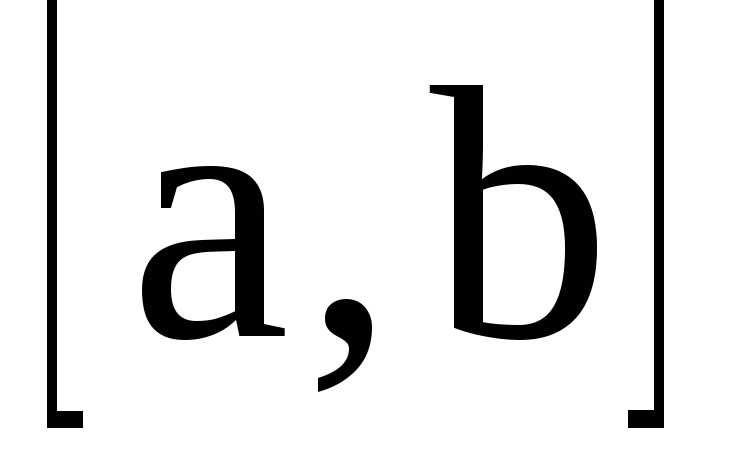В
большинстве случаев решать эту задачу
приходится приближенно численными
методами, которые основаны на замене
подынтегральной функции
интерполяционным многочленом. Для
достижения необходимой точности
вычислений интервал интегрирования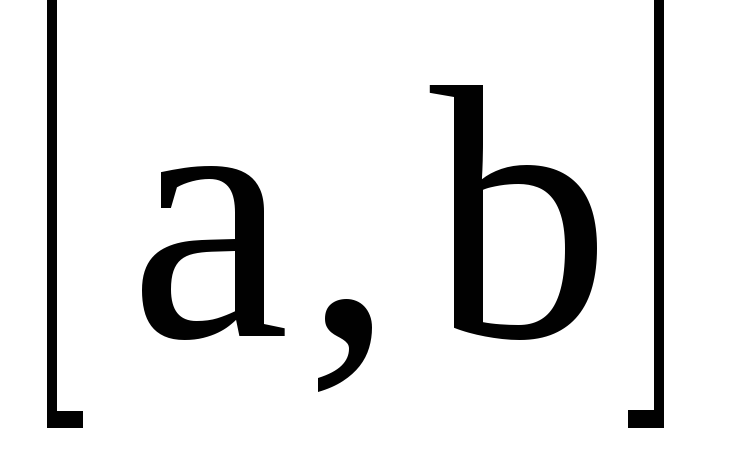делится на более мелкие частии на каждом из этих участков производится
соответствующая замена. Тогда весь
интеграл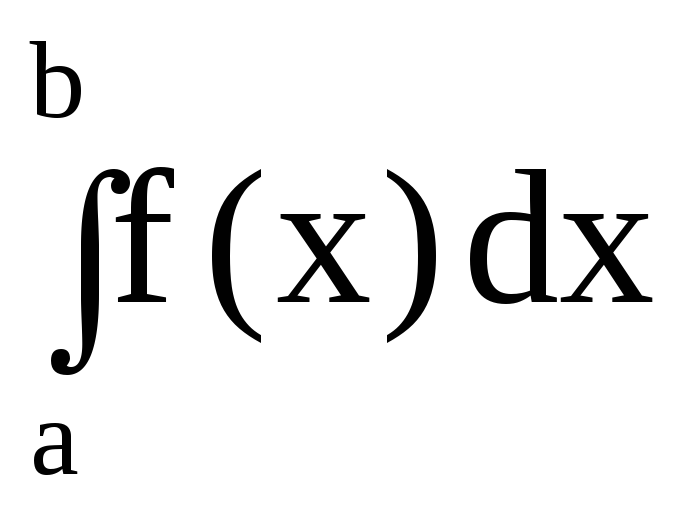представляется в виде линейной комбинации
нескольких значений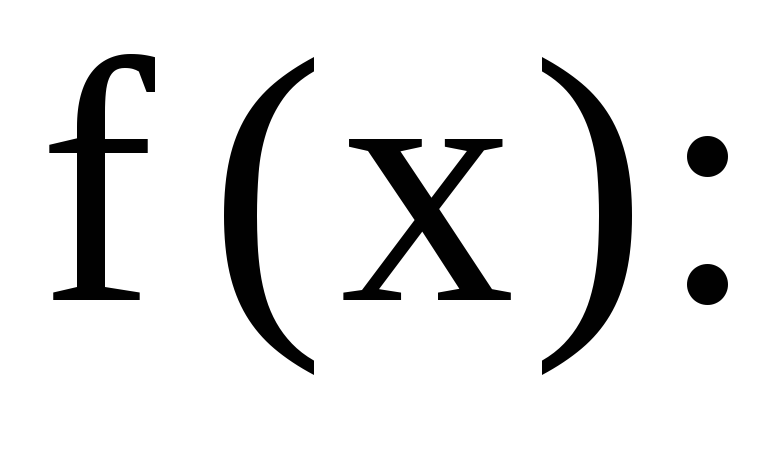

При
фиксированном n

или

(1)

Формулы
вида (1) называются квадратурными.

называется
остаточным членом.

Значения

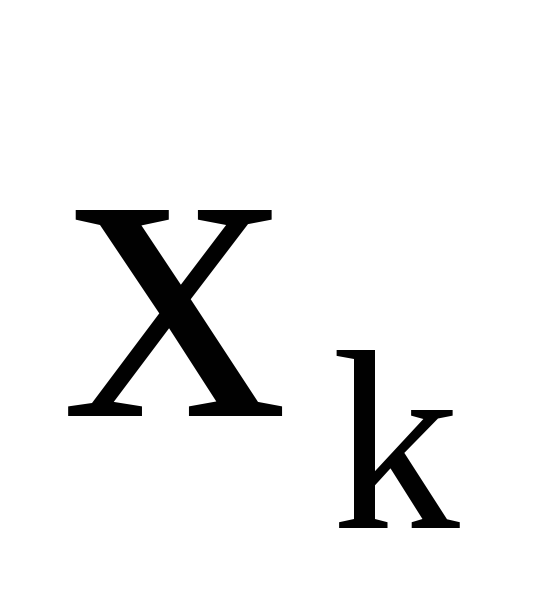называются узлами или сеткой,n–
число разбиений интервала интегрирования.

Если

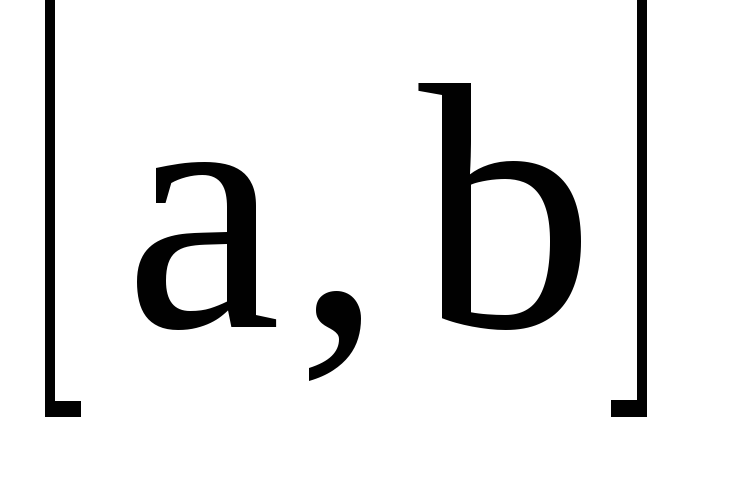делится на равные части, то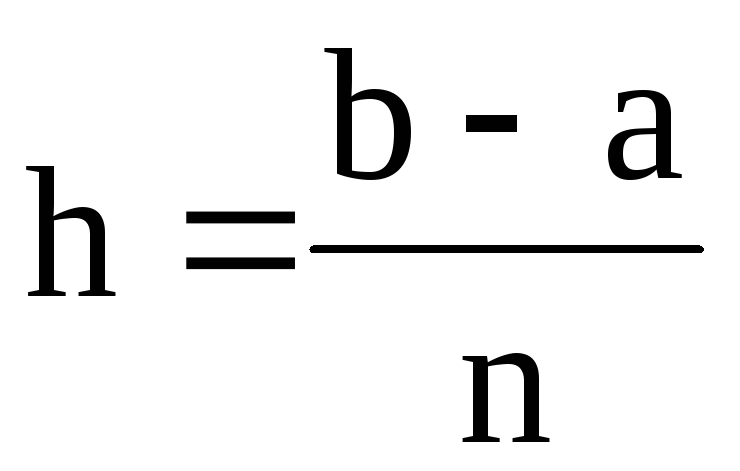называется шагом сетки.

Приближенное
значение интеграла будет зависеть от
h,
поэтому будем обозначать его J(h).

Справочная информация

История

Вычислительная математика возникла довольно давно. Ещё в Древней Месопотамии были разработаны методы получения квадратного корня. В эпоху научной революции вычислительная математика развивалась быстрыми темпами из практических применений параллельно с математическим анализом. Помимо этого, подобные вычисления широко применялись в небесной механике для предсказания траектории движения небесных тел. Это привело к появлению таких важнейших составляющих физики, как теория о гелиоцентрической системе устройства мира, законы Кеплера и законы Ньютона. XVII и XVIII век стали временем разработки значительного количества численных методов и алгоритмов.

Применение большого количества инженерных вычислений в XIX и XX веках потребовало создания соответствующих приборов. Одним из таких приборов стала логарифмическая линейка, также появились таблицы значений функций с точностью до 16 знаков после запятой, помогавшие проводить вычисления. Также существовали механические устройства для выполнения математических операций, называвшиеся арифмометрами. В первой половине XX века для решения дифференциальных уравнений стали активно использоваться аналоговые ЭВМ.

Изобретение компьютера в середине XX века означало создание универсального инструмента для математических вычислений. Совместно с мейнфреймами в распоряжении инженеров и учёных для выполнения ручных операций были только калькуляторы, которые активно использовались вплоть до начала массового производства персональных компьютеров.