Математический калькулятор

Танки других стран

Сравнительные ТТХ современных основных танков

	Т-90А	БМ «Оплот»	Абрамс M1A2 SEP	Леопард 2A6M	AMX-56 Леклерк	Челленджер 2	Ариете	PT-91M

Внешний вид
Год принятия на вооружение	2005	2009	2000	2004	1992	2002	1995	2010
Боевая масса, т	46,5	51,0	63,0	68,5	54,6	62,5	54,0	45,5
Экипаж	3	3	4	4	3	4	4	3
Калибр пушки, мм	125	125	120	120	120	120	120	125
Панорамный прицел	нет	ПНК-6	есть	PERI-R-12	SFIM VS-580	SFIM VS-580	ATTILA	нет
Управляемое вооружение	Рефлекс-М	Комбат	нет	нет	нет	нет	нет	нет
Боекомплект, выстрелов	43	46	42	42	40	52	42	40
Скорострельность, выстр/мин	7	8	н/д	н/д	10—12	н/д	н/д	7
Динамическая защита	Контакт-5	Дуплет	TUSK ARAT	есть	нет	ROMOR	нет	ERAWA
Активная защита	Штора-1	Варта	AN/VLQ-6 MCD / Трофи	MUSS	н/д	н/д	н/д	OBRA-3
Мощность двигателя, л. с.	1000	1200	1500	1500	1500	1200	1275	1000
Удельная мощность, л. с./т	21,5	23,5	23,8	24,0	27,5	19,2	23,6	22,0
Максимальная скорость, км/ч	60…70	70	67	72	72	56	65	65
Запас хода по шоссе, км	550…700	500	425	550	550	400	550	480

	Меркава Mk.4М	Арджун Mk.I	Аль-Халид	Зульфикар	Сонгун-915	K2	Тип 99А2	Тип 10

Внешний вид
Год принятия на вооружение	2009	2011	2001	1997	2009	2014	2011	2012
Боевая масса, т	65,0	58,5	48,0	36,0	44	55,0	58,0	44,0
Экипаж	4	4	3	3	н/д	3	3	3
Калибр пушки, мм	120	120	125	125	125	120	125	120
Панорамный прицел	есть	нет	есть	нет	нет	есть	есть	есть
Управляемое вооружение	LAHAT	LAHAT	нет	нет	Bulsae-3	KSTAM	Рефлекс	нет
Боекомплект, выстрелов	48	39	39	н/д	н/д	н/д	41	н/д
Скорострельность, выстр/мин	н/д	6—8	8	н/д	н/д	10	7	н/д
Динамическая защита	есть	нет	есть	нет	есть	есть	есть	нет
Активная защита	Трофи	нет	Варта	нет	нет	есть	JD-3	н/д
Мощность двигателя, л. с.	1500	1400	1200	780	1200	1500	1500	1200
Удельная мощность, л. с./т	23,5	23,9	25,0	21,7	27,3	27,3	25,9	27,3
Максимальная скорость, км/ч	70	70	70	70	70	70	70	70
Запас хода по шоссе, км	500	450	500	450	н/д	450	450	н/д

Основные понятия

Во всем мире принято использовать эти десять цифр для записи чисел: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. С их помощью создается любое натуральное число.

Название числа напрямую зависит от количества знаков.

• Однозначное — состоит из одного знака
• Двузначное — из двух
• Трехзначное — из трех и так далее.

Разряд — это позиция, на которой стоит цифра в записи. Их принято отсчитываются с конца.

Разряд единиц — то, чем заканчивается любое число. Разряд десятков — то, что находится перед разрядом единиц. Разряд сотен стоит перед разрядом десятков. На место отсутствующего разряда всегда можно поставить ноль.

В числе 429 содержится 0 тысяч, 4 сотни, 2 десятка и 9 единиц.

Умножение — арифметическое действие в котором участвуют два аргумента. Один множимый, второй множитель. Результат их умножения называется произведением.

Свойства умножения Калькулятор юнит-экономики от jetstyle: зачем он нужен и как пользоваться 1. От перестановки множителей местами произведение не меняется. a * b = b * a 2. Результат произведения трёх и более множителей не изменится, если любую группу заменить произведением. a * b * c = (a * b) * c = a * (b * c) Самое главное в процессе вычисления — это знание таблицы умножения. Это сделает подсчет упорядоченным и быстрым.

Важно помнить правило: умножение в столбик с нулями дает в результате ноль

а * 0 = 0, где а — любое натуральное число.

Алгоритм умножения в столбик

Чтобы понять, как умножать в столбик — рассмотрим действия по шагам:

1. Запишем пример в строку. Выберем и подчеркнем из двух чисел наименьшее, чтобы не забыть при новой записи поставить его вниз.

2. Записываем произведение в виде столбика. Сначала наибольший множитель, затем наименьший, тот что мы подчеркнули ранее. Слева ставим соответствующий знак и проводим черту под которой будем записывать ход решения

Важно обратить внимание разряды, чтобы единицы стояли стоять под единицами, десятки под десятками и т. д

3. Поэтапно производим необходимые действия. Каждую цифру первого множителя нужно умножить на крайнюю цифру второго. Это действие происходит справа налево: единицы, десятки, сотни.

Если результат получится двузначным, под чертой записывается только последняя его цифра. Остальное переносим в следующий разряд путем сложения со значением, полученным при следующем умножении.

4. После умножения на единицу второго множителя с остальными цифрами необходимо провести аналогичные манипуляции. Результаты записывать под чертой, сдвигаясь влево на одну позицию.

5. Складываем то, что нашли и получаем ответ.

Умножение на однозначное число

Для решения задачи по произведению двух натуральных чисел, одно из которых однозначное, а другое — многозначное, нужно использовать способ столбика. Для вычисления воспользуемся последовательностью шагов, которую рассмотрели выше. 

Возьмем пример 234 * 2:

1. Запишем первый множитель, а под ним второй. Соответствующие разряды расположены друг под другом. Двойка находится под четверкой.

2. Последовательно умножаем каждое число в первом множителе на второй, начиная с единиц и продвигаясь к десяткам и сотням.

3. Ответ запишем под чертой:

Производить действия необходимо в следующей последовательности: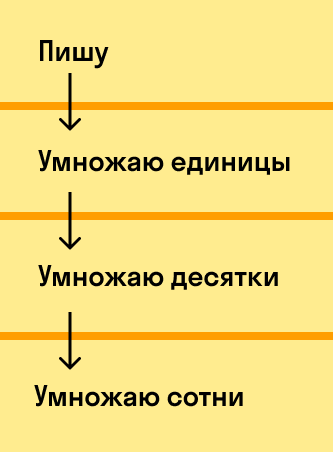

Умножение двух многозначных чисел

Если оба множителя — многозначные натуральные числа, нужно действовать следующим образом.

Рассмотрим пример 207 * 8063:

1. Сначала запишем наибольшее 8063, затем наименьшее 207. Нужно разместить цифры друг под другом справа налево:

1. Последовательно перемножаем значения разрядов. Результатом является неполное произведение.

1. Далее перемножаем десятки. Первый множитель умножим на значение разряда десятков второго и т.д. Результат запишем под чертой.

1. По аналогии действуем с сотыми. Ноль пропускаем в соответствии с правилом. Так получилось второе неполное произведение:

1. Далее складываем два произведения в столбик. 

1. Получившееся семизначное число — результат умножения исходных натуральных чисел.

Ответ: 8 063 * 207 = 1669041. 

Примеры на умножение в столбик

Самостоятельное решение задачек помогает быстрее запомнить правила и натренировать скорость

Неважно, в каком классе учится ребенок — в 1, 3 или 4 — эти примеры подойдут всем

Чтобы запомнить все правила, повторите метод сложения столбиком, так как один из этапов умножения состоит из сложения промежуточных результатов. А еще лучше — приходите заниматься увлекательной математикой в детскую школу Skysmart.

Вместо скучных параграфов ученики решают интерактивные задачки и головоломки с мгновенной автоматической проверкой, а еще чертят фигуры на онлайн-доске вместе с преподавателем.

Шаги

Метод 1 из 3:

Умножение корней без множителей

1. 1

   Убедитесь, что корни имеют одинаковый показатель (степень). Степень записывается слева над знаком корня. Если степени нет, то корень считается квадратным (то есть его степень равна 2) и его можно умножить на другие квадратные корни (об умножении корней с разными показателями читайте далее). Вот несколько примеров умножения корней с одинаковыми показателями:

   • Пример 1: √(18) x √(2) = ?
   • Пример 2: √(10) x √(5) = ?
   • Пример 3: 3√(3) x 3√(9) = ?

2. 2

   Перемножьте числа под корнем. Вот как это делается:

   • Пример 1: √(18) x √(2) = √(36)
   • Пример 2: √(10) x √(5) = √(50)
   • Пример 3: 3√(3) x 3√(9) = 3√(27)

3. 3

   Упростите подкоренное выражение. При умножении корней полученное подкоренное выражение можно упростить (не всегда) до произведения некоторого числа (или выражения) на полный квадрат или куб. Вот как это делается:

   • Пример 1: √(36) = 6. 36 является квадратом числа 6, потому что 6*6=36.
   • Пример 2

     Если внести число 5 обратно под знак корня, оно возводится в квадрат, и вы получите число 25 под знаком корня.

     : √(50) = √(25*2) = √(*2) = 5√(2). Число 50 можно разложить на произведение чисел 25 и 2. Корень из 25 равен 5, поэтому выносим 5 за знак корня и таким образом упрощаем подкоренное выражение.

   • Пример 3: 3√(27) = 3. Кубический корень из числа 27 равен 3, потому что 3*3*3 = 27.

Метод 2 из 3:

Умножение корней с множителями

1. 1

   Умножьте множители. Множитель — число, стоящее перед знаком корня. Если его нет, то множитель равен 1. Перемножьте множители. Вот как это делается:

   • Пример 1

     3 x 1 = 3

     : 3√(2) x √(10) = 3√(?)

   • Пример 2

     4 x 3 = 12

     : 4√(3) x 3√(6) = 12√(?)

2. 2

   Умножьте числа под знаком корня. После того как вы перемножили множители, перемножьте числа под знаком корня. Вот как это делается:

   • Пример 1: 3√(2) x √(10) = 3√(2 x 10) = 3√(20)
   • Пример 2: 4√(3) x 3√(6) = 12√(3 x 6) = 12√(18)

3. 3

   Упростите подкоренное выражение. Далее упростите полученные значения под знаком корня, вынеся соответствующие числа за знак корня. После этого просто перемножьте эти вынесенные числа и множители, стоящие перед знаком корня. Вот как это делается:

   • 3√(20) = 3√(4 x 5) = 3√( x 5) = (3 x 2)√(5) = 6√(5)
   • 12√(18) = 12√(9 x 2) = 12√(3 x 3 x 2) = (12 x 3)√(2) = 36√(2)

Метод 3 из 3:

Умножение корней с разными показателями

1. 1

   Найдите НОК (наименьшее общее кратное) показателей. НОК показателей — наименьшее число, которое делится на оба показателя. Найдите НОК показателей для следующего выражения:3√(5) x 2

   Показатели равны 3 и 2. Число 6 является НОК этих двух чисел, потому что это наименьшее число, которое делится без остатка как на 3, так и на 2: 6/3=2 и 6/2=3. Чтобы умножить корни, их показатель должен быть равен 6.

   √(2) = ?

2. 2

   Запишите каждый корень с НОК в качестве нового показателя.

   6√(5) x 6√(2) = ?

   Вот как записать выражение с новым показателем:

3. 3

   Найдите числа, на которые необходимо умножить каждый исходный показатель, чтобы получить НОК. В выражении 3√(5) вам нужно умножить показатель 3 на 2, чтобы получить 6. В выражении 2√(2) вам нужно умножить показатель 2 на 3, чтобы получить 6.

4. 4

   Возведите число, стоящее под знаком корня, в степень равную числу, найденному в предыдущем шаге. Для первого выражения возведите 5 в степень 2. Для второго выражения возведите 2 в степень 3. Вот как это будет выглядеть:

   • 2 —> 6√(5) = 6√(5)2
   • 3 —> 6√(2) = 6√(2)3

5. 5

   Проделайте операцию возведения в степень и запишите результат под знаком корня. Вот как это делается:

   • 6√(5)2 = 6√(5 x 5) = 6√25
   • 6√(2)3 = 6√(2 x 2 x 2) = 6√8

6. 6

   Перемножьте числа под знаком корня: 6√(8 x 25)

7. 7

   Запишите ответ. 6√(8 x 25) = 6√(200). В некоторых случаях можно упростить подкоренное выражение, например, найдя множитель числа 200, из которого можно взять корень 6 степени. Но в данном случае выражение не упрощается.

• Если «множитель» отделяется от корня знаком плюс или минус, то это уже вообще не множитель — это отдельный член выражения, и операции с ним проводятся отдельно от корня.
• Знак корня является еще одним способом записи дробных показателей. Например, квадратный корень из любого числа есть это число в степени 1/2; кубический корень из любого числа есть это число в степени 1/3 и так далее.
• Множитель — число, стоящее непосредственно перед знаком корня. Так, например, в выражении 2(квадратный корень)5, число 5 является подкоренным выражением, а число 2 — множителем. Когда множитель и корень записаны рядом, то это означает их умножение: 2*(квадратный корень)5.

Игра 3

Выбираем традиционные методы

Проверенные десятилетиями способы перемножения двузначных чисел не теряют своей актуальности. Простейшие приемы помогают миллионам обычных школьников, учащихся специализированных ВУЗов и лицеев, а также людям, занимающимся саморазвитием, усовершенствовать вычислительное мастерство.

Умножение с помощью разложения чисел

Наиболее легким способом, как быстро научиться умножать большие числа в уме, является перемножение десятков и единиц. Сначала умножаются десятки двух чисел, затем поочередно единицы и десятки. Четыре полученных числа суммируются

Для использования этого метода важно уметь запоминать результаты перемножения и складывать их в уме

Например, для умножения 38 на 57 необходимо:

• разложить число на (30+8)*(50+7);
• 30*50 = 1500 – запомнить результат;
• 30*7 + 50*8 = 210 + 400 = 610 – запомнить;
• (1500 + 610) + 8*7 = 2110 + 56 = 2166

Естественно, необходимо отлично знать таблицу умножения, так как быстро умножать в уме этим способом не удастся без соответствующих умений.

Умножение в столбик в уме

Визуальное представление привычного перемножения в столбик многие используют при расчетах. Этот метод подойдет тем, кто умеет надолго запоминать вспомогательные числа и выполнять с ними арифметические действия. Но процесс значительно упрощается, если вы научились, как быстро умножать двузначные числа на однозначные. Для перемножения, например, 47*81 нужно:

• 47*1 = 47 – запомнить;
• 47*8 = 376 – запоминаем;
• 376*10 + 47 = 3807.

Запоминать промежуточные результаты поможет проговаривание их вслух с одновременным суммированием в уме. Несмотря на сложность мысленных вычислений, после непродолжительных тренировок этот метод станет вашим любимым.

Приведенные выше способы умножения универсальны. Но знание более эффективных алгоритмов для некоторых чисел намного сократит количество расчетов.

Умножение на 11

Это, пожалуй, самый простой способ, который используется для умножения любых двузначных чисел на 11.

Достаточно между цифрами множителя вставить их сумму:13*11 = 1(1+3)3 = 143

Если в скобках получается число больше 10, то к первой цифре добавляется единица, а из суммы в скобках вычитается 10.28*11 = 2 (2+8) 8 = 308

Умножение больших чисел

Очень удобно перемножать числа, близкие к 100 разложением их на составляющие. Например, необходимо умножить 87 на 91.

• Каждое число необходимо представить как разницу 100 и еще одного числа:(100 — 13)*(100 — 9) Ответ будет состоять из четырех цифр, две первые из которых – разница первого множителя и вычитаемого из второй скобки или наоборот – разница второго множителя и вычитаемого из первой скобки.87 – 9 = 78 91 – 13 = 78
• Вторые две цифры ответа — результат перемножения вычитаемых из двух скобок.

  13*9 = 144

• В результате получаются числа 78 и 144. Если при записывании окончательного результата получается число из 5 цифр вторую и третью цифру суммируем.

  Результат: 87*91 = 7917.

Это самые простые способы перемножения. После многократного их применения, доведения вычислений до автоматизма можно осваивать более сложные техники. И через некоторое время проблема, как быстро умножить двузначные числа перестанет вас волновать, а память и логика существенно улучшатся.

Коронавирус в России статистика онлайн

Пишем математические стихи

Все дети, как известно, разные. И все они обладают своими способностями. Одни из них прекрасно оперируют цифрами и усваивают их законы. Другие по натуре лирики. И сколько им ни объясняй логику умножения чисел, они мало что способны понять и запомнить. Поэтому существуют маленькие ученики, для которых легко запомнить таблицу умножения в стихах. Как это сделать лучше?

Прежде всего следует обратить внимание ребенка, что некоторые задачи с умножением и ответы на них рифмуются сами по себе. Приведем примеры подобного:

Приведем примеры подобного:

• пятью пять – двадцать пять;

• шестью шесть – тридцать шесть;

• семью пять – тридцать пять;

• девятью пять – сорок пять.

Но если даже задачи сразу не складываются в рифмы, то можно дописать их, то есть добавить фразы, тем самым сотворив из них стихотворение.

Здесь в качестве примера рассмотрим таблицу умножения на 7. А стишок может быть таким:

Семью два – четырнадцать, я хочу ученым стать;

Семью три – двадцать один, мы упорно посидим;

Семью четыре – двадцать восемь, сами решим, ни у кого не спросим;

Семью пять – тридцать пять, сто раз я повторю опять;

Семью шесть – сорок два, помогают мне учить слова;

Семью семь – сорок девять, главное работу сделать;

Семью восемь – пятьдесят шесть, я уверен, так оно и есть;

Семью девять – шестьдесят три, и это правильно, что ни говори.

Самое главное при претворении данного метода в жизнь для родителей – понимать, что не надо детям предлагать готовые рифмованные строчки, заставляя бездумно зазубривать их. Лучше совместно попытаться сочинить свои стихи и подобрать удачные рифмы. Только тогда можно говорить об уверенности в том, что ребенок прекрасно заучит таблицу умножения и запомнит ее на всю оставшуюся жизнь.

Выбор оголовка

Пожалуй, основной особенностью, которую необходимо учитывать при выборе изделия – это его диаметр. Данная особенность при выборе является основополагающей.

На сегодняшний день диаметр обсадных труб подбирается в соответствии с глубинным насосом для скважин, который будет осуществлять добычу воды.Цена изделия зависит, как правило, от его диаметра и материала. Стоимость колеблется в пределах 90 – 160 мм.

Маркировка изделия

Для простоты выбора, производители зашифровывают характеристики изделия в его маркировку.

На рынке чаще всего можно встретить оголовки от следующих производителей:

• «Водолей»;
• «Джилекс»;
• «Merrill».

Оголовок «Водолей» 133 – 32

В названии этих изделий указывается маркировка типа -ОС 90-110/25 Плибо ОС 133 — 32. Р

асшифровывается она следующим образом:

• ОС – аббревиатура слов:«оголовок скважинный».
• 90 – 110 или 133 – означает диаметры обсадных труб, для которых можно использовать изделие. Соответственно, марки типа 90-110 являются универсальными, рассчитанными на трубы разного диаметра.
• Последние цифры «40, 32 или 25» – обозначают диаметр переходников под трубы водопровода.
• Если в названии имеется буква «П» – то это значит, что оголовок выполнен из пластика. Если буквы «П» в названии нет, значит оголовок сделан из стали или чугуна.

К примеру, оголовок «Водолей» ОС 100 – 32 подходит для обсадных труб диаметром 100 мм и имеет переходник под трубы водопровода диаметром 32 мм.

Устройство скважины

• Скважинный уровнемер
• Крышка для скважины

Красивая речь и положение в обществе

Как посчитать проценты, составив пропорцию

Составлять пропорции — одно из наиболее полезных умений, которому вас научили в школе. С его помощью можно посчитать любые проценты. Выглядит пропорция так:

сумма, составляющая 100% : 100% = часть суммы : доля в процентном соотношении.

Или можно записать её так: a : b = c : d.

Обычно пропорция читается как «а относится к b так же, как с относится к d». Произведение крайних членов пропорции равно произведению её средних членов. Чтобы узнать неизвестное число из этого равенства, нужно решить простейшее уравнение.

Пример 1

Для примера вычислений используем рецепт быстрого брауни. Вы хотите его приготовить и купили подходящую плитку шоколада массой 90 г, но не удержались и откусили кусочек-другой. Теперь у вас только 70 г шоколада, и вам нужно узнать, сколько масла положить вместо 200 г.

Сначала вычисляем процентную долю оставшегося шоколада.

90 г : 100% = 70 г : Х, где Х — масса оставшегося шоколада.

Х = 70 × 100 / 90 = 77,7%.

Теперь составляем пропорцию, чтобы выяснить, сколько масла нам нужно:

200 г : 100% = Х : 77,7%, где Х — нужное количество масла.

Х = 77,7 × 200 / 100 = 155,4.

Следовательно, в тесто нужно положить примерно 155 г масла.

Пример 2

Пропорция подойдёт и для расчёта выгодности скидок. Например, вы видите блузку за 1 499 рублей со скидкой 13%.

Сначала узнайте, сколько стоит блузка в процентах. Для этого отнимите 13 от 100 и получите 87%.

Составьте пропорцию: 1 499 : 100 = Х : 87.

Х = 87 × 1 499 / 100.

Заплатите 1 304,13 рубля и носите блузку с удовольствием.

«Нефть, золото или медь?» — самые влиятельные активы товарно-сырьевого рынка

В форме игры

Изучение такого материала всухую — не интересно. Ваша задача — ребенка заинтересовать, пробудить в нем энтузиазм и желание узнать что-то новое!

Реальные примеры

Ребенку будет намного интереснее и понятнее, ели объяснить умножение на реальных примерах. Допустим, у мальчика можно спросить, сколько колес вместе у 6 автомобилей, а девочку — сколько ног у 5 кукол.

Также можно использовать и подручные материалы: карандаши, кубики, тетради. Например, поставьте по 6 карандашей в несколько стаканов и объясните, что общее их количество это сумма карандашей в одном стакане умноженная на 2 стакана.

Использование рифмы

Те примеры, которые даются школьнику с трудом (как правило, на большие числа) можно изучать с помощью стишков. Это могут быть как рифмы на сами числа, например: «семь у восемь = сорок восемь», так и стишки с другими словами, которые ребенок запомнит, например: «Жабки говорили «ква», а восемь на девять = семьдесят два»

Таблица на цветочках

С девочками примеры умножения можно учить на бумажных цветочках с лепесточками, как на рисунке ниже. В серединке цветка напишите число, на которое нужно умножать, а на лепестках — числа от 1 до 10 по кругу. Правильный ответ напишите под лепестком, и увидеть его можно, только отогнув бумажку. Так ребенок будет учиться в игровой форме и сразу себя проверять.

Изучение по карточкам

Также эффективной формой изучения являются карточки. Из картона сделайте множество простых карточек с примерами на каждую цифру без ответа и показывайте ее ребенку. Если школьник дал правильный ответ — карточка «уходит» из игры, ели ошибся — возвращается в колоду. Игра заканчивается тогда, когда ребенок даст правильные ответы на все примеры.

Также можно играть на время или подсчитывать свои неправильные и правильные ответы, чтобы каждый день пытаться побить рекорд. Играть можно и от обратного, когда на карточках пишите только ответ, а ребенок должен назвать несколько примеров, которые в результате умножения дадут это число. Но такая игра будет интересна в том случае, если он уже хорошо усвоил таблицу, а не только в начале пути к ее осмыслению.

Веселые домики

Для изучения таблицы умножения в игровой форме можно склеить вот такие забавные домики с окошками в разных вариантах. С их помощью примеры можно видеть перед глазами и сразу себя проверять, заглядывая в окошки, где прячется правильный ответ.

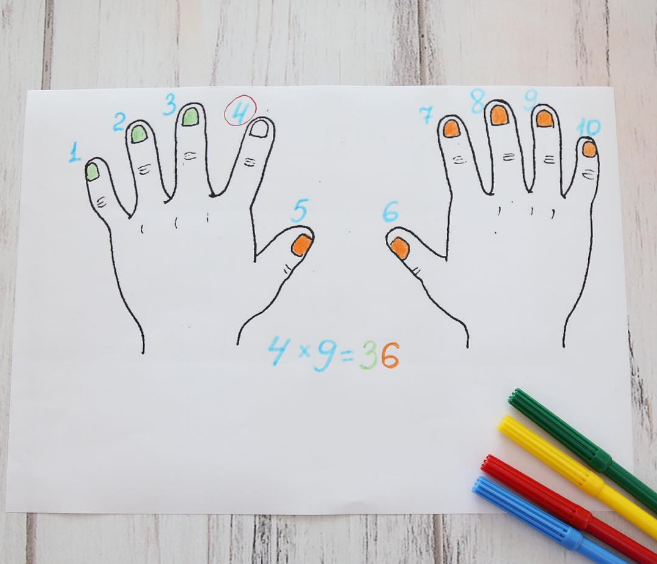
Считаем на пальцах

С помощью пальцев рук можно легко научиться умножать на цифру 9! При этом ребенку не нужно будет никаких подсказок. Все, что нужно сделать это посчитать от левого большого пальца до числа, которое мы умножаем на 9.

Если посмотреть на картинку, то зеленые пальчики — это десятки, а оранжевые — единицы.

Например: 4х9

Считаем: 3 пальца слева до 4-го и 6 пальцев слева после 4-го. Складываем — получается 36. Проверьте с ребенком эту теорию, умножая таким образом на 9 любое число.

Умножение многозначных чисел на многозначные

Умножение многозначных чисел на многозначные происходит таким же образом, как и умножение многозначных на однозначные. Каждая цифра многозначного числа умножается на каждую цифру другого многозначного числа. Единственное отличие заключается в том, что в конце образуется своего рода лесенка ответов, которые надо сложить. Рассмотрим несколько примеров, чтобы хорошо понять это.

Пример 1. Найти значение выражения 12 × 14

Записываем данное выражение в столбик — единицы под единицами, десятки десятками:

Теперь умножаем каждую цифру числа 12 на каждую цифру числа 14. Делать это надо по-очереди, начав с четвёрки. В результате таких действий мы приходим к умножению многозначного числа на однозначное, которое проходили ранее:

Умножив 12 на 4, мы получили число 48, которое записали таким образом, чтобы разряд единиц этого числа оказался под четверкой, на которую мы умножали число 12.

Теперь умножаем 12 на 1:

Умножив 12 на 1 мы получили число 12 и записали его таким образом, чтобы разряд единиц этого числа оказался под единицей, на которую мы умножали число 12.

Мы получили лесенку ответов 48 и 12, которую надо сложить. Складываем и получаем ответ 168

В данном примере множитель 14 это четыре единицы и один десяток. Тогда умножение 12 на 14 можно понимать как увеличение числа 12 в четыре раза и в десять раз. Этим и объясняется появление лесенки в конце решения. Давайте посмотрим как это выглядит на каждом этапе:

Увеличим число 12 в четыре раза, получим число 48

Увеличим число 12 в десять раз, получим число 120. Записываем 120 так, чтобы можно было сложить единицы этого числа с единицами числа 48, а десятки числа 120 можно было сложить с десятками числа 48

Теперь сложим получившуюся лесенку ответов. Единицы сложим с единицами, десятки с десятками, сотни с сотнями. В результате образуется окончательный ответ:

Но чаще всего множитель не группируется с помощью разрядов, и умножение выполняют, умножая каждую цифру множимого на каждую цифру множителя.

Пример 2. Найти значение выражения 25 × 36

Записываем данное выражение в столбик

Умножаем каждую цифру числа 25 на каждую цифру числа 36.

Умножим 25 на 6:

Умножаем 25 на 3:

Теперь сложим получившуюся лесенку:

Получили ответ 900.

Рассмотрим большой и сложный пример на умножение: 12305 × 5641. Будем придерживаться ранее изученных правил.

Сначала записываем в столбик данное выражение

Теперь начинаем умножать. Число 12305 надо умножить на каждую цифру числа 5641.

Умножив 12305 на 1, мы получили 12305 и записали это число так, чтобы разряд единиц этого числа оказался под единицей, на которую мы умножили 12305.

Теперь умножаем 12305 на следующую цифру 4:

Умножив 12305 на 4, мы получили 49220 и записали это число так, чтобы разряд единиц этого числа оказался под четверкой, на которую умножали 12305.

Умножаем 12305 на следующую цифру 6:

Умножив 12305 на 6, мы получили 73830 и записали это число так, чтобы разряд единиц этого числа оказался под шестёркой, на которую мы умножали 12305.

Теперь умножаем 12305 на последнюю цифру 5:

Умножив 12305 на 5, мы получили 61525 и записали это число так, чтобы разряд единиц этого числа оказался под пятёркой, на которую умножали 12305.

В результате мы получили большую лесенку, которую надо сложить. Складываем:

Получили окончательный ответ 69412505.

Если вы поняли этот пример, то можно сказать, что умножение больших чисел вы усвоили на отлично.

На этом урок по умножению можно завершить. Обязательно потренируйтесь, решив несколько примеров, которые даны ниже.

Важно отметить, что все эти стрелки и подробные решения, как на картинках в «боевых условиях» рисовать не принято. Нужно уметь сразу записывать ответы, выполняя в уме все вычисления

Исключением является то, если человек давно не занимался математикой или никогда ею не занимался. В таком случае можно рисовать для себя стрелки и другие вспомогательные схемы для хорошего усвоения материала.